Error function

Not to be confused with Loss function.

In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a function defined as:

$$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t.$$

Error function
Plot of the error function
General information
General definition	$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t$
Fields of application	Probability, thermodynamics, digital communications
Domain, codomain and image
Domain	$\mathbb {R}$
Image	$\left(-1,1\right)$
Basic features
Parity	Odd
Specific features
Root	0
Derivative	Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}}
Antiderivative	$\int \operatorname {erf} z\,dz=z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}+C$
Series definition
Taylor series	$\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}$

In some old texts, the error function is defined without the factor of $2/{\sqrt {\pi }}$. This nonelementary integral is a sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.

In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation $1/{\sqrt {2}}$, erf x is the probability that Y falls in the range [−x, x].

Two closely related functions are the complementary error function (erfc) defined as Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \operatorname {erfc} z=1-\operatorname {erf} z,} and the imaginary error function (erfi) defined as

$$\operatorname {erfi} z=-i\operatorname {erf} iz,$$

where i is the imaginary unit.

Name

The name "error function" and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with "the theory of Probability, and notably the theory of Errors." The error function complement was also discussed by Glaisher in a separate publication in the same year. For the "law of facility" of errors whose density is given by

$$f(x)=\left({\frac {c}{\pi }}\right)^{1/2}e^{-cx^{2}}$$

(the normal distribution), Glaisher calculates the probability of an error lying between p and q as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{c}{\pi}\right)^\frac{1}{2} \int_p^qe^{-cx^2}\,\mathrm dx = \tfrac{1}{2}\left(\operatorname{erf} \left(q\sqrt{c}\right) -\operatorname{erf} \left(p\sqrt{c}\right)\right).}

Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

Applications

When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (⁠a/σ √2⁠) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.

The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.

The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L > μ, it can be shown via integration by substitution: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Pr[X\leq L] &= \frac{1}{2} + \frac{1}{2} \operatorname{erf}\frac{L-\mu}{\sqrt{2}\sigma} \\ &\approx A \exp \left(-B \left(\frac{L-\mu}{\sigma}\right)^2\right) \end{align}}

where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pr[X\leq L] \leq A \exp (-B \ln{k}) = \frac{A}{k^B}}

so the probability goes to 0 as k → ∞.

The probability for X being in the interval [L_a, L_b] can be derived as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Pr[L_a\leq X \leq L_b] &= \int_{L_a}^{L_b} \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \,\mathrm dx \\ &= \frac{1}{2}\left(\operatorname{erf}\frac{L_b-\mu}{\sqrt{2}\sigma} - \operatorname{erf}\frac{L_a-\mu}{\sqrt{2}\sigma}\right).\end{align}}

Properties

Plots in the complex plane

Integrand exp(−z²)

erf z

The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e^−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).

Since the error function is an entire function which takes real numbers to real numbers, for any complex number z: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} \overline{z} = \overline{\operatorname{erf} z} } where z is the complex conjugate of z.

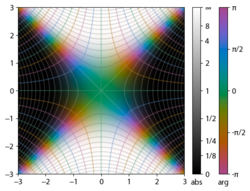
The integrand f = exp(−z²) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.

The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.

Taylor series

The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges. For x >> 1, however, cancellation of leading terms makes the Taylor expansion unpractical.

The defining integral cannot be evaluated in closed form in terms of elementary functions (see Liouville's theorem), but by expanding the integrand e^−z2 into its Maclaurin series and integrating term by term, one obtains the error function's Maclaurin series as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erf} z &= \frac{2}{\sqrt\pi}\sum_{n=0}^\infty\frac{(-1)^n z^{2n+1}}{n! (2n+1)} \\[6pt] &= \frac{2}{\sqrt\pi} \left(z-\frac{z^3}{3}+\frac{z^5}{10}-\frac{z^7}{42}+\frac{z^9}{216}-\cdots\right) \end{align}} which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.

For iterative calculation of the above series, the following alternative formulation may be useful: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erf} z &= \frac{2}{\sqrt\pi}\sum_{n=0}^\infty\left(z \prod_{k=1}^n {\frac{-(2k-1) z^2}{k (2k+1)}}\right) \\[6pt] &= \frac{2}{\sqrt\pi} \sum_{n=0}^\infty \frac{z}{2n+1} \prod_{k=1}^n \frac{-z^2}{k} \end{align}} because ⁠−(2k − 1)z²/k(2k + 1)⁠ expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).

The imaginary error function has a very similar Maclaurin series, which is:

$${\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}$$

which holds for every complex number z.

Derivative and integral

The derivative of the error function follows immediately from its definition: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mathrm d}{\mathrm dz}\operatorname{erf} z =\frac{2}{\sqrt\pi} e^{-z^2}.} From this, the derivative of the imaginary error function is also immediate: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d}{dz}\operatorname{erfi} z =\frac{2}{\sqrt\pi} e^{z^2}.} An antiderivative of the error function, obtainable by integration by parts, is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\operatorname{erf}z + \frac{e^{-z^2}}{\sqrt\pi}.} An antiderivative of the imaginary error function, also obtainable by integration by parts, is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\operatorname{erfi}z - \frac{e^{z^2}}{\sqrt\pi}.} Higher order derivatives are given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf}^{(k)}z = \frac{2 (-1)^{k-1}}{\sqrt\pi} \mathit{H}_{k-1}(z) e^{-z^2} = \frac{2}{\sqrt\pi} \frac{\mathrm d^{k-1}}{\mathrm dz^{k-1}} \left(e^{-z^2}\right),\qquad k=1, 2, \dots} where H are the physicists' Hermite polynomials.

Bürmann series

An expansion, which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann's theorem: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erf} x &= \frac{2}{\sqrt\pi} \sgn x \cdot \sqrt{1-e^{-x^2}} \left( 1-\frac{1}{12} \left (1-e^{-x^2} \right ) -\frac{7}{480} \left (1-e^{-x^2} \right )^2 -\frac{5}{896} \left (1-e^{-x^2} \right )^3-\frac{787}{276 480} \left (1-e^{-x^2} \right )^4 - \cdots \right) \\[10pt] &= \frac{2}{\sqrt\pi} \sgn x \cdot \sqrt{1-e^{-x^2}} \left(\frac{\sqrt\pi}{2} + \sum_{k=1}^\infty c_k e^{-kx^2} \right). \end{align}} where sgn is the sign function. By keeping only the first two coefficients and choosing c₁ = ⁠31/200⁠ and c₂ = −⁠341/8000⁠, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x \approx \frac{2}{\sqrt\pi}\sgn x \cdot \sqrt{1-e^{-x^2}} \left(\frac{\sqrt{\pi}}{2} + \frac{31}{200}e^{-x^2}-\frac{341}{8000} e^{-2x^2}\right). }

Inverse functions

Inverse error function

Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf⁻¹ x satisfying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf}\left(\operatorname{erf}^{-1} x\right) = x.}

The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series

$$\operatorname {erf} ^{-1}z=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},$$

where c₀ = 1 and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} c_k & =\sum_{m=0}^{k-1}\frac{c_m c_{k-1-m}}{(m+1)(2m+1)} \\[1ex] &= \left\{1,1,\frac{7}{6},\frac{127}{90},\frac{4369}{2520},\frac{34807}{16200},\ldots\right\}. \end{align}}

So we have the series expansion (common factors have been canceled from numerators and denominators): Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf}^{-1} z = \frac{\sqrt{\pi}}{2} \left (z + \frac{\pi}{12}z^3 + \frac{7\pi^2}{480}z^5 + \frac{127\pi^3}{40320}z^7 + \frac{4369\pi^4}{5806080} z^9 + \frac{34807\pi^5}{182476800}z^{11} + \cdots\right ).} (After cancellation the numerator and denominator values in OEIS: A092676 and OEIS: A092677 respectively; without cancellation the numerator terms are values in OEIS: A002067.) The error function's value at ±∞ is equal to ±1.

For |z| < 1, we have erf(erf⁻¹ z) = z.

The inverse complementary error function is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc}^{-1}(1-z) = \operatorname{erf}^{-1} z.} For real x, there is a unique real number erfi⁻¹ x satisfying erfi(erfi⁻¹ x) = x. The inverse imaginary error function is defined as erfi⁻¹ x.

For any real x, Newton's method can be used to compute erfi⁻¹ x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfi}^{-1} z =\sum_{k=0}^\infty\frac{(-1)^k c_k}{2k+1} \left( \frac{\sqrt\pi}{2} z \right)^{2k+1},} where c_k is defined as above.

Asymptotic expansion

A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erfc} x &= \frac{e^{-x^2}}{x\sqrt{\pi}}\left(1 + \sum_{n=1}^\infty (-1)^n \frac{1\cdot3\cdot5\cdots(2n - 1)}{\left(2x^2\right)^n}\right) \\[6pt] &= \frac{e^{-x^2}}{x\sqrt{\pi}}\sum_{n=0}^\infty (-1)^n \frac{(2n - 1)!!}{\left(2x^2\right)^n}, \end{align}} where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc} x = \frac{e^{-x^2}}{x\sqrt{\pi}}\sum_{n=0}^{N-1} (-1)^n \frac{(2n - 1)!!}{\left(2x^2\right)^n} + R_N(x)} where the remainder is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_N(x) := \frac{(-1)^N}{\sqrt\pi} 2^{1 - 2N}\frac{(2N)!}{N!}\int_x^\infty t^{-2N}e^{-t^2}\,\mathrm dt,} which follows easily by induction, writing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-t^2} = -(2t)^{-1}\left(e^{-t^2}\right)'} and integrating by parts.

The asymptotic behavior of the remainder term, in Landau notation, is Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle R_{N}(x)=O\left(x^{-(1+2N)}e^{-x^{2}}\right)} as x → ∞. This can be found by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_N(x) \propto \int_x^\infty t^{-2N}e^{-t^2}\,\mathrm dt = e^{-x^2} \int_0^\infty (t+x)^{-2N}e^{-t^2-2tx}\,\mathrm dt\leq e^{-x^2} \int_0^\infty x^{-2N} e^{-2tx}\,\mathrm dt \propto x^{-(1+2N)}e^{-x^2}.} For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).

Continued fraction expansion

A continued fraction expansion of the complementary error function is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc} z = \frac{z}{\sqrt\pi}e^{-z^2} \cfrac{1}{z^2+ \cfrac{a_1}{1+\cfrac{a_2}{z^2+ \cfrac{a_3}{1+\dotsb}}}},\qquad a_m = \frac{m}{2}.}

Factorial series

The inverse factorial series: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erfc} z &= \frac{e^{-z^2}}{\sqrt{\pi}\,z} \sum_{n=0}^\infty \frac{\left(-1\right)^n Q_n}{{\left(z^2+1\right)}^{\bar{n}}} \\[1ex] &= \frac{e^{-z^2}}{\sqrt{\pi}\,z} \left[1 -\frac{1}{2}\frac{1}{(z^2+1)} + \frac{1}{4}\frac{1}{\left(z^2+1\right) \left(z^2+2\right)} - \cdots \right] \end{align}} converges for Re(z²) > 0. Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} Q_n &\overset{\text{def}}{{}={}} \frac{1}{\Gamma{\left(\frac{1}{2}\right)}} \int_0^\infty \tau(\tau-1)\cdots(\tau-n+1)\tau^{-\frac{1}{2}} e^{-\tau} \,d\tau \\[1ex] &= \sum_{k=0}^n \left(\frac{1}{2}\right)^{\bar{k}} s(n,k), \end{align}} zⁿ denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind. There also exists a representation by an infinite sum containing the double factorial: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} z = \frac{2}{\sqrt\pi} \sum_{n=0}^\infty \frac{(-2)^n(2n-1)!!}{(2n+1)!}z^{2n+1}}

Numerical approximations

Approximation with elementary functions

• Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x \approx 1 - \frac{1}{\left(1 + a_1x + a_2x^2 + a_3x^3 + a_4x^4\right)^4}, \qquad x \geq 0} (maximum error: 5×10⁻⁴)

  where a₁ = 0.278393, a₂ = 0.230389, a₃ = 0.000972, a₄ = 0.078108

  $$\operatorname {erf} x\approx 1-\left(a_{1}t+a_{2}t^{2}+a_{3}t^{3}\right)e^{-x^{2}},\quad t={\frac {1}{1+px}},\qquad x\geq 0$$
  (maximum error: 2.5×10⁻⁵)

  where p = 0.47047, a₁ = 0.3480242, a₂ = −0.0958798, a₃ = 0.7478556

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x \approx 1 - \frac{1}{\left(1 + a_1x + a_2x^2 + \cdots + a_6x^6\right)^{16}}, \qquad x \geq 0} (maximum error: 3×10⁻⁷)

  where a₁ = 0.0705230784, a₂ = 0.0422820123, a₃ = 0.0092705272, a₄ = 0.0001520143, a₅ = 0.0002765672, a₆ = 0.0000430638

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x \approx 1 - \left(a_1t + a_2t^2 + \cdots + a_5t^5\right)e^{-x^2},\quad t = \frac{1}{1 + px}} (maximum error: 1.5×10⁻⁷)

  where p = 0.3275911, a₁ = 0.254829592, a₂ = −0.284496736, a₃ = 1.421413741, a₄ = −1.453152027, a₅ = 1.061405429

  All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).

• Exponential bounds and a pure exponential approximation for the complementary error function are given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erfc} x &\leq \frac{1}{2}e^{-2 x^2} + \frac{1}{2}e^{- x^2} \leq e^{-x^2}, &\quad x &> 0 \\[1.5ex] \operatorname{erfc} x &\approx \frac{1}{6}e^{-x^2} + \frac{1}{2}e^{-\frac{4}{3} x^2}, &\quad x &> 0 . \end{align}}
• The above have been generalized to sums of N exponentials with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{Q}(x) = \sum_{n=1}^N a_n e^{-b_n x^2}.} In particular, there is a systematic methodology to solve the numerical coefficients {(a_n,b_n)}^N
  _{n = 1} that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(a_n,b_n)}^N
  _{n = 1} for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.
• A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007) who showed for the appropriate choice of parameters {A,B} that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc} x \approx \frac{\left(1 - e^{-Ax}\right)e^{-x^2}}{B\sqrt{\pi} x}.} They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.
• A single-term lower bound is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc} x \geq \sqrt{\frac{2 e}{\pi}} \frac{\sqrt{\beta - 1}}{\beta} e^{- \beta x^2}, \qquad x \ge 0,\quad \beta > 1,} where the parameter β can be picked to minimize error on the desired interval of approximation.
• Another approximation is given by Sergei Winitzki using his "global Padé approximations": Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x \approx \sgn x \cdot \sqrt{1 - \exp\left(-x^2\frac{\frac{4}{\pi} + ax^2}{1 + ax^2}\right)}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = \frac{8(\pi - 3)}{3\pi(4 - \pi)} \approx 0.140012.} This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.

  This approximation can be inverted to obtain an approximation for the inverse error function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf}^{-1}x \approx \sgn x \cdot \sqrt{\sqrt{\left(\frac{2}{\pi a} + \frac{\ln\left(1 - x^2\right)}{2}\right)^2 - \frac{\ln\left(1 - x^2\right)}{a}} -\left(\frac{2}{\pi a} + \frac{\ln\left(1 - x^2\right)}{2}\right)}.}

• An approximation with a maximal error of 1.2×10⁻⁷ for any real argument is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x = \begin{cases} 1-\tau & x\ge 0\\ \tau-1 & x < 0 \end{cases}} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \tau &= t\cdot\exp\left(-x^2-1.26551223+1.00002368 t+0.37409196 t^2+0.09678418 t^3 -0.18628806 t^4\right.\\ &\left. \qquad\qquad\qquad +0.27886807 t^5-1.13520398 t^6+1.48851587 t^7 -0.82215223 t^8+0.17087277 t^9\right) \end{align}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \frac{1}{1 + \frac{1}{2}|x|}.}
• An approximation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc}} with a maximum relative error less than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{-53}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\approx 1.1 \times 10^{-16}\right)} in absolute value is: for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\ge 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{aligned} \operatorname{erfc} \left(x\right) & = \left(\frac{0.56418958354775629}{x+2.06955023132914151}\right) \left(\frac{x^2+2.71078540045147805 x+5.80755613130301624}{x^2+3.47954057099518960 x+12.06166887286239555}\right) \\ & \left(\frac{x^2+3.47469513777439592 x+12.07402036406381411}{x^2+3.72068443960225092 x+8.44319781003968454}\right) \left(\frac{x^2+4.00561509202259545 x+9.30596659485887898}{x^2+3.90225704029924078 x+6.36161630953880464}\right) \\ & \left(\frac{x^2+5.16722705817812584 x+9.12661617673673262}{x^2+4.03296893109262491 x+5.13578530585681539}\right) \left(\frac{x^2+5.95908795446633271 x+9.19435612886969243}{x^2+4.11240942957450885 x+4.48640329523408675}\right) e^{-x^2} \\ \end{aligned}} and for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc} \left(x\right) = 2 - \operatorname{erfc} \left(-x\right)}
• A simple approximation for real-valued arguments could be done through Hyperbolic functions:
  $$\operatorname {erf} \left(x\right)\approx z(x)=\tanh \left({\frac {2}{\sqrt {\pi }}}\left(x+{\frac {11}{123}}x^{3}\right)\right)$$
  which keeps the absolute difference Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\operatorname{erf} \left(x\right)-z(x)\right| < 0.000358,\, \forall x} .

Table of values

Further information: Interval estimation, Coverage probability, and 68–95–99.7 rule

x	erf x	1 − erf x
0	0	1
0.02	0.022564575	0.977435425
0.04	0.045111106	0.954888894
0.06	0.067621594	0.932378406
0.08	0.090078126	0.909921874
0.1	0.112462916	0.887537084
0.2	0.222702589	0.777297411
0.3	0.328626759	0.671373241
0.4	0.428392355	0.571607645
0.5	0.520499878	0.479500122
0.6	0.603856091	0.396143909
0.7	0.677801194	0.322198806
0.8	0.742100965	0.257899035
0.9	0.796908212	0.203091788
1	0.842700793	0.157299207
1.1	0.880205070	0.119794930
1.2	0.910313978	0.089686022
1.3	0.934007945	0.065992055
1.4	0.952285120	0.047714880
1.5	0.966105146	0.033894854
1.6	0.976348383	0.023651617
1.7	0.983790459	0.016209541
1.8	0.989090502	0.010909498
1.9	0.992790429	0.007209571
2	0.995322265	0.004677735
2.1	0.997020533	0.002979467
2.2	0.998137154	0.001862846
2.3	0.998856823	0.001143177
2.4	0.999311486	0.000688514
2.5	0.999593048	0.000406952
3	0.999977910	0.000022090
3.5	0.999999257	0.000000743

Related functions

Complementary error function

The complementary error function, denoted erfc, is defined as

Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

$${\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}$$

which also defines erfcx, the scaled complementary error function (which can be used instead of erfc to avoid arithmetic underflow). Another form of erfc x for x ≥ 0 is known as Craig's formula, after its discoverer: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc} (x \mid x\ge 0) = \frac{2}{\pi} \int_0^\frac{\pi}{2} \exp \left( - \frac{x^2}{\sin^2 \theta} \right) \, \mathrm d\theta.} This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erfc} (x+y \mid x,y\ge 0) = \frac{2}{\pi} \int_0^\frac{\pi}{2} \exp \left( - \frac{x^2}{\sin^2 \theta} - \frac{y^2}{\cos^2 \theta} \right) \,\mathrm d\theta.}

Imaginary error function

The imaginary error function, denoted erfi, is defined as

Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erfi} x & = -i\operatorname{erf} ix \\[5pt] & = \frac{2}{\sqrt\pi} \int_0^x e^{t^2}\,\mathrm dt \\[5pt] & = \frac{2}{\sqrt\pi} e^{x^2} D(x), \end{align} } where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow).

Despite the name "imaginary error function", erfi x is real when x is real.

When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(z) = e^{-z^2}\operatorname{erfc}(-iz) = \operatorname{erfcx}(-iz).}

Cumulative distribution function

The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages, as they differ only by scaling and translation. Indeed,

the normal cumulative distribution function plotted in the complex plane

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Phi(x) &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^\tfrac{-t^2}{2}\,\mathrm dt\\[6pt] &= \frac{1}{2} \left(1+\operatorname{erf}\frac{x}{\sqrt 2}\right)\\[6pt] &= \frac{1}{2} \operatorname{erfc}\left(-\frac{x}{\sqrt 2}\right) \end{align}} or rearranged for erf and erfc: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \operatorname{erf}(x) &= 2 \Phi \left ( x \sqrt{2} \right ) - 1 \\[6pt] \operatorname{erfc}(x) &= 2 \Phi \left ( - x \sqrt{2} \right ) \\ &=2\left(1-\Phi \left ( x \sqrt{2} \right)\right). \end{align}}

Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} Q(x) &= \frac{1}{2} - \frac{1}{2} \operatorname{erf} \frac{x}{\sqrt 2}\\ &= \frac{1}{2}\operatorname{erfc}\frac{x}{\sqrt 2}. \end{align}}

The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{probit}(p) = \Phi^{-1}(p) = \sqrt{2}\operatorname{erf}^{-1}(2p-1) = -\sqrt{2}\operatorname{erfc}^{-1}(2p).}

The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.

The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer's function): Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x = \frac{2x}{\sqrt\pi} M\left(\tfrac{1}{2},\tfrac{3}{2},-x^2\right).}

It has a simple expression in terms of the Fresnel integral.

In terms of the regularized gamma function P and the incomplete gamma function, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{erf} x = \sgn x \cdot P\left(\tfrac{1}{2}, x^2\right) = \frac{\sgn x}{\sqrt\pi} \gamma{\left(\tfrac{1}{2}, x^2\right)}.} sgn x is the sign function.

Iterated integrals of the complementary error function

The iterated integrals of the complementary error function are defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i^n\!\operatorname{erfc} z &= \int_z^\infty i^{n-1}\!\operatorname{erfc} \zeta\,\mathrm d\zeta \\[6pt] i^0\!\operatorname{erfc} z &= \operatorname{erfc} z \\ i^1\!\operatorname{erfc} z &= \operatorname{ierfc} z = \frac{1}{\sqrt\pi} e^{-z^2} - z \operatorname{erfc} z \\ i^2\!\operatorname{erfc} z &= \tfrac{1}{4} \left( \operatorname{erfc} z -2 z \operatorname{ierfc} z \right) \\ \end{align}}

The general recurrence formula is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 n \cdot i^n\!\operatorname{erfc} z = i^{n-2}\!\operatorname{erfc} z -2 z \cdot i^{n-1}\!\operatorname{erfc} z}

They have the power series Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^n\!\operatorname{erfc} z =\sum_{j=0}^\infty \frac{(-z)^j}{2^{n-j}j! \,\Gamma \left( 1 + \frac{n-j}{2}\right)},} from which follow the symmetry properties Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{2m}\!\operatorname{erfc} (-z) =-i^{2m}\!\operatorname{erfc} z +\sum_{q=0}^m \frac{z^{2q}}{2^{2(m-q)-1}(2q)! (m-q)!}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{2m+1}\!\operatorname{erfc}(-z) =i^{2m+1}\!\operatorname{erfc} z +\sum_{q=0}^m \frac{z^{2q+1}}{2^{2(m-q)-1}(2q+1)! (m-q)!}. }

Implementations

As real function of a real argument

• In POSIX-compliant operating systems, the header math.h shall declare and the mathematical library libm shall provide the functions erf and erfc (double precision) as well as their single precision and extended precision counterparts erff, erfl and erfcf, erfcl.
• The GNU Scientific Library provides erf, erfc, log(erf), and scaled error functions.

As complex function of a complex argument

• libcerf, numeric C library for complex error functions, provides the complex functions cerf, cerfc, cerfcx and the real functions erfi, erfcx with approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package

Further reading

• Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 7". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
• Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), "Section 6.2. Incomplete Gamma Function and Error Function", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, archived from the original on 11 August 2011, retrieved 9 August 2011
• Temme, Nico M. (2010), "Error Functions, Dawson's and Fresnel Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.

External links

• A Table of Integrals of the Error Functions