File:Integer multiplication by FFT.svg
Size of this PNG preview of this SVG file: 666 × 580 pixels. Other resolutions: 276 × 240 pixels | 551 × 480 pixels | 882 × 768 pixels | 1,176 × 1,024 pixels | 2,352 × 2,048 pixels.
Original file (SVG file, nominally 666 × 580 pixels, file size: 79 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
This SVG image was uploaded in a graphics format such as GIF, PNG, JPEG, or SVG. However, it consists purely or largely of information which is better suited to representation in wikitext (possibly using MediaWiki's special syntax for tables, math, or music). This will make the information easier to edit, as well as make it accessible to users of screen readers and text-based browsers.
If possible, please replace any inclusions of this image in articles (noted under the “File links” header) with properly formatted wikitext. After doing so, please consider nominating this image for deletion. Deutsch ∙ English ∙ +/− |
Summary
| DescriptionInteger multiplication by FFT.svg |
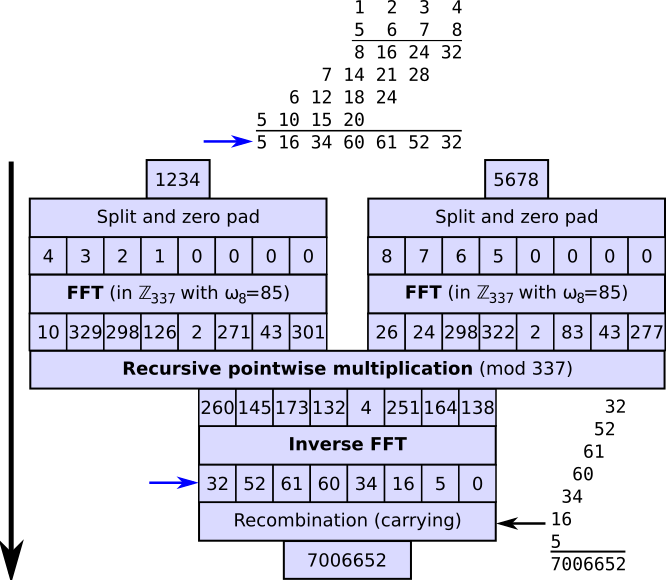
English: A demonstration of an integer multiplication based on fast Fourier transforms (FFTs) using a number theoretic transform in the finite field of order 337, choosing 85 as an 8th root of unity (since the input vectors are of length 8). Base 10 is used (normally a power of 2 would used, but 10 is convenient for demonstration), and this technique is overkill for integers of this size (long multiplication would be superior). Because the inputs have 4 digits and the maximum product of two digits in base 10 is 92, the base was chosen as the first prime p greater than 4×92 = 324 where 8 is invertible in the integers modulo p (in this example any suitable base > 61, such as 73, would suffice, but we don't know that a priori). The computation at the top shows how the same acyclic convolution can be computed naively by "long multiplication without carrying," showing the relationship to multiplication. The computation in the lower right shows recombination/carrying of the result vector by (decimal) shifts and adds to obtain the final integer result. Note that all recursive multiplications are of smaller, 3-digit integers. Values are all accurate and were computed using the following Mathematica code:
NTT[x_, b_, r_] :=
Table[Mod[Sum[x[[n + 1]]*PowerMod[r, k*n, b], {n, 0, Length[x] - 1}],
b], {k, 0, Length[x] - 1}]
INTT[x_, b_, r_] := Block[{ninverse},
ninverse = PowerMod[Length[x], -1, b];
Table[Mod[
ninverse*
Sum[x[[n + 1]]*PowerMod[r, (Length[x] - n)*k, b], {n, 0,
Length[x] - 1}], b], {k, 0, Length[x] - 1}]]
x = {4, 3, 2, 1, 0, 0, 0, 0}; y = {8, 7, 6, 5, 0, 0, 0, 0}; b = 337; r = 85;
NTT[x, b, r]
NTT[y, b, r]
Mod[NTT[x, b, r]*NTT[y, b, r], b]
INTT[Mod[NTT[x, b, r]*NTT[y, b, r], b], b, r]
1234*5678
|
| Date | |
| Source | Own work |
| Author | Dcoetzee |
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
17 December 2011
image/svg+xml
80,688 byte
3cf0b512af9956dc77fd39417abe7b67ac0ee3db
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 11:37, 17 December 2011 |  | 666 × 580 (79 KB) | wikimediacommons>Dcoetzee |
File usage
The following page uses this file: