Dimension (vector space)

In mathematics, the dimension of a vector space V is the cardinality (i.e., the number of vectors) of a basis of V over its base field. It is sometimes called Hamel dimension (after Georg Hamel) or algebraic dimension to distinguish it from other types of dimension.

A diagram of dimensions 1, 2, 3, and 4

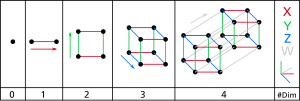
For every vector space there exists a basis, and all bases of a vector space have equal cardinality; as a result, the dimension of a vector space is uniquely defined. We say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is finite-dimensional if the dimension of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is finite, and infinite-dimensional if its dimension is infinite.

The dimension of the vector space $V$ over the field $F$ can be written as $\dim _{F}(V)$ or as $[V:F],$ read "dimension of $V$ over $F$". When $F$ can be inferred from context, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim(V)} is typically written.

Examples

The vector space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^3} has Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\right\}} as a standard basis, and therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim_{\R}(\R^3) = 3.} More generally, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim_{\R}(\R^n) = n,} and even more generally, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim_{F}(F^n) = n} for any field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F.}

The complex numbers $\mathbb {C}$ are both a real and complex vector space; we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim_{\R}(\Complex) = 2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim_{\Complex}(\Complex) = 1.} So the dimension depends on the base field.

The only vector space with dimension Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{0\},} the vector space consisting only of its zero element.

Properties

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} is a linear subspace of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim (W) \leq \dim (V).}

To show that two finite-dimensional vector spaces are equal, the following criterion can be used: if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is a finite-dimensional vector space and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W} is a linear subspace of $V$ with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim (W) = \dim (V),} then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = V.}

The space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^n} has the standard basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{e_1, \ldots, e_n\right\},} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_i} is the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} -th column of the corresponding identity matrix. Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R^n} has dimension $n.$

Any two finite dimensional vector spaces over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} with the same dimension are isomorphic. Any bijective map between their bases can be uniquely extended to a bijective linear map between the vector spaces. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} is some set, a vector space with dimension Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |B|} over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} can be constructed as follows: take the set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(B)} of all functions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f : B \to F} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(b) = 0} for all but finitely many $b$ in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B.} These functions can be added and multiplied with elements of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} to obtain the desired Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} -vector space.

An important result about dimensions is given by the rank–nullity theorem for linear maps.

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F / K} is a field extension, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} is in particular a vector space over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K.} Furthermore, every Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} -vector space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is also a $K$-vector space. The dimensions are related by the formula Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim_K(V) = \dim_K(F) \dim_F(V).} In particular, every complex vector space of dimension Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is a real vector space of dimension Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2n.}

Some formulae relate the dimension of a vector space with the cardinality of the base field and the cardinality of the space itself. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is a vector space over a field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} and if the dimension of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim V,} then:

If dim Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is finite then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |V| = |F|^{\dim V}.}

If dim Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is infinite then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |V| = \max (|F|, \dim V).}

Generalizations

A vector space can be seen as a particular case of a matroid, and in the latter there is a well-defined notion of dimension. The length of a module and the rank of an abelian group both have several properties similar to the dimension of vector spaces.

The Krull dimension of a commutative ring, named after Wolfgang Krull (1899–1971), is defined to be the maximal number of strict inclusions in an increasing chain of prime ideals in the ring.

Trace

See also: Trace (linear algebra)

The dimension of a vector space may alternatively be characterized as the trace of the identity operator. For instance, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \operatorname{tr}\ \operatorname{id}_{\R^2} = \operatorname{tr} \left(\begin{smallmatrix} 1 & 0 \\ 0 & 1 \end{smallmatrix}\right) = 1 + 1 = 2.} This appears to be a circular definition, but it allows useful generalizations.

Firstly, it allows for a definition of a notion of dimension when one has a trace but no natural sense of basis. For example, one may have an algebra Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} with maps $\eta :K\to A$ (the inclusion of scalars, called the unit) and a map Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon : A \to K} (corresponding to trace, called the counit). The composition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \circ \eta : K \to K} is a scalar (being a linear operator on a 1-dimensional space) corresponds to "trace of identity", and gives a notion of dimension for an abstract algebra. In practice, in bialgebras, this map is required to be the identity, which can be obtained by normalizing the counit by dividing by dimension (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon := \textstyle{\frac{1}{n}} \operatorname{tr}} ), so in these cases the normalizing constant corresponds to dimension.

Alternatively, it may be possible to take the trace of operators on an infinite-dimensional space; in this case a (finite) trace is defined, even though no (finite) dimension exists, and gives a notion of "dimension of the operator". These fall under the rubric of "trace class operators" on a Hilbert space, or more generally nuclear operators on a Banach space.

A subtler generalization is to consider the trace of a family of operators as a kind of "twisted" dimension. This occurs significantly in representation theory, where the character of a representation is the trace of the representation, hence a scalar-valued function on a group Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi : G \to K,} whose value on the identity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \in G} is the dimension of the representation, as a representation sends the identity in the group to the identity matrix: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi(1_G) = \operatorname{tr}\ I_V = \dim V.} The other values Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi(g)} of the character can be viewed as "twisted" dimensions, and find analogs or generalizations of statements about dimensions to statements about characters or representations. A sophisticated example of this occurs in the theory of monstrous moonshine: the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} -invariant is the graded dimension of an infinite-dimensional graded representation of the monster group, and replacing the dimension with the character gives the McKay–Thompson series for each element of the Monster group.

See also

• Fractal dimension – Ratio providing a statistical index of complexity variation with scale
• Krull dimension – In mathematics, dimension of a ring
• Matroid rank – Maximum size of an independent set of the matroid
• Rank (linear algebra) – Dimension of the column space of a matrix
• Topological dimension, also called Lebesgue covering dimension

Sources

• Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 978-3-319-11079-0.

External links

• MIT Linear Algebra Lecture on Independence, Basis, and Dimension by Gilbert Strang at MIT OpenCourseWare