Summation

This article is about sums of several elements. For more elementary aspects, see Addition. For infinite sums, see Series (mathematics). For other uses, see Summation (disambiguation).

In mathematics, summation is the addition of a sequence of numbers, called addends or summands; the result is their sum or total. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined.

Summations of infinite sequences are called series. They involve the concept of limit, and are not considered in this article.

The summation of an explicit sequence is denoted as a succession of additions. For example, summation of [1, 2, 4, 2] is denoted 1 + 2 + 4 + 2, and results in 9, that is, 1 + 2 + 4 + 2 = 9. Because addition is associative and commutative, there is no need for parentheses, and the result is the same irrespective of the order of the summands. Summation of a sequence of only one element results in this element itself. Summation of an empty sequence (a sequence with no elements), by convention, results in 0.

Very often, the elements of a sequence are defined, through a regular pattern, as a function of their place in the sequence. For simple patterns, summation of long sequences may be represented with most summands replaced by ellipses. For example, summation of the first 100 natural numbers may be written as 1 + 2 + 3 + 4 + ⋯ + 99 + 100. Otherwise, summation is denoted by using Σ notation, where ${\textstyle \sum }$ is an enlarged capital Greek letter sigma. For example, the sum of the first n natural numbers can be denoted as ${\textstyle \sum _{i=1}^{n}i}$.

For long summations, and summations of variable length (defined with ellipses or Σ notation), it is a common problem to find closed-form expressions for the result. For example,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n i = \frac{n(n+1)}{2}.}

Although such formulas do not always exist, many summation formulas have been discovered—with some of the most common and elementary ones being listed in the remainder of this article.

Notation

Further information: Iterated binary operation § Notation

Capital-sigma notation

The summation symbol

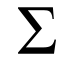
Mathematical notation uses a symbol that compactly represents summation of many similar terms: the summation symbol, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \sum} , an enlarged form of the upright capital Greek letter sigma. This is defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i \mathop =m}^n a_i = a_m + a_{m+1} + a_{m+2} + \cdots + a_{n-1} + a_n}

where i is the index of summation; a_i is an indexed variable representing each term of the sum; m is the lower bound of summation, and n is the upper bound of summation. The "i = m" under the summation symbol means that the index i starts out equal to m. The index, i, is incremented by one for each successive term, stopping when i = n.

This is read as "sum of a_i, from i = m to n".

Here is an example showing the summation of squares:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i = 3}^6 i^2 = 3^2+4^2+5^2+6^2 = 86.}

In general, while any variable can be used as the index of summation (provided that no ambiguity is incurred), some of the most common ones include letters such as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , $k$, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} ; the latter is also often used for the upper bound of a summation.

Alternatively, index and bounds of summation are sometimes omitted from the definition of summation if the context is sufficiently clear. This applies particularly when the index runs from 1 to n. For example, one might write that:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum a_i^2 = \sum_{i = 1}^n a_i^2.}

Generalizations of this notation are often used, in which an arbitrary logical condition is supplied, and the sum is intended to be taken over all values satisfying the condition. For example:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{0 \le k < 100} f(k)}

is an alternative notation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \sum_{k = 0}^{99} f(k),} the sum of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(k)} over all (integers) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} in the specified range. Similarly,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{x \mathop \in S} f(x)}

is the sum of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} over all elements Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} in the set $S$, and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{d\,|\,n}\;\mu(d)}

is the sum of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu(d)} over all positive integers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} dividing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .

There are also ways to generalize the use of many sigma signs. For example,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i,j}}

is the same as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i}\sum_{j}.}

A similar notation is used for the product of a sequence, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \prod} , an enlarged form of the Greek capital letter pi, is used instead of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \sum.}

Special cases

It is possible to sum fewer than 2 numbers:

• If the summation has one summand Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , then the evaluated sum is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .
• If the summation has no summands, then the evaluated sum is zero, because zero is the identity for addition. This is known as the empty sum.

These degenerate cases are usually only used when the summation notation gives a degenerate result in a special case. For example, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=m} in the definition above, then there is only one term in the sum; if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=m-1} , then there is none.

Algebraic sum

The phrase 'algebraic sum' refers to a sum of terms which may have positive or negative signs. Terms with positive signs are added, while terms with negative signs are subtracted.

Formal definition

Summation may be defined recursively as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=a}^b g(i)=0} , for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b<a } ;

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=a}^b g(i)=g(b)+\sum_{i=a}^{b-1} g(i)} , for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \geqslant a} .

Measure theory notation

In the notation of measure and integration theory, a sum can be expressed as a definite integral,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k \mathop =a}^b f(k) = \int_{[a,b]} f\,d\mu}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a, b]} is the subset of the integers from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} , and where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} is the counting measure over the integers.

Calculus of finite differences

Given a function f that is defined over the integers in the interval [m, n], the following equation holds:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(n)-f(m)= \sum_{i=m}^{n-1} (f(i+1)-f(i)).}

This is known as a telescoping series and is the analogue of the fundamental theorem of calculus in calculus of finite differences, which states that:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(n)-f(m)=\int_m^n f'(x)\,dx,}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}}

is the derivative of f.

An example of application of the above equation is the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^k=\sum_{i=0}^{n-1} \left((i+1)^k-i^k\right).}

Using binomial theorem, this may be rewritten as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^k=\sum_{i=0}^{n-1} \biggl(\sum_{j=0}^{k-1} \binom{k}{j} i^j\biggr).}

The above formula is more commonly used for inverting of the difference operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} , defined by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta(f)(n)=f(n+1)-f(n), }

where f is a function defined on the nonnegative integers. Thus, given such a function f, the problem is to compute the antidifference of f, a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=\Delta^{-1}f} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta F=f} . That is, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(n+1)-F(n)=f(n).} This function is defined up to the addition of a constant, and may be chosen as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(n)=\sum_{i=0}^{n-1} f(i).}

There is not always a closed-form expression for such a summation, but Faulhaber's formula provides a closed form in the case where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(n)=n^k} and, by linearity, for every polynomial function of n.

Approximation by definite integrals

Many such approximations can be obtained by the following connection between sums and integrals, which holds for any increasing function f:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{s=a-1}^{b} f(s)\ ds \le \sum_{i=a}^{b} f(i) \le \int_{s=a}^{b+1} f(s)\ ds.}

and for any decreasing function f:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{s=a}^{b+1} f(s)\ ds \le \sum_{i=a}^{b} f(i) \le \int_{s=a-1}^{b} f(s)\ ds.}

For more general approximations, see the Euler–Maclaurin formula.

For summations in which the summand is given (or can be interpolated) by an integrable function of the index, the summation can be interpreted as a Riemann sum occurring in the definition of the corresponding definite integral. One can therefore expect that for instance

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{b-a}{n}\sum_{i=0}^{n-1} f\left(a+i\frac{b-a}n\right) \approx \int_a^b f(x)\ dx,}

since the right-hand side is by definition the limit for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\to\infty} of the left-hand side. However, for a given summation n is fixed, and little can be said about the error in the above approximation without additional assumptions about f: it is clear that for wildly oscillating functions the Riemann sum can be arbitrarily far from the Riemann integral.

Identities

The formulae below involve finite sums; for infinite summations or finite summations of expressions involving trigonometric functions or other transcendental functions, see list of mathematical series.

General identities

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=s}^t C\cdot f(n) = C\cdot \sum_{n=s}^t f(n) \quad} (distributivity)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=s}^t f(n) \pm \sum_{n=s}^{t} g(n) = \sum_{n=s}^t \left(f(n) \pm g(n)\right)\quad} (commutativity and associativity)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=s}^t f(n) = \sum_{n=s+p}^{t+p} f(n-p)\quad} (index shift)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n\in B} f(n) = \sum_{m\in A} f(\sigma(m)), \quad} for a bijection σ from a finite set A onto a set B (index change); this generalizes the preceding formula.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=s}^t f(n) =\sum_{n=s}^j f(n) + \sum_{n=j+1}^t f(n)\quad} (splitting a sum, using associativity)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=a}^{b}f(n)=\sum_{n=0}^{b}f(n)-\sum_{n=0}^{a-1}f(n)\quad} (a variant of the preceding formula)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=s}^t f(n) = \sum_{n=0}^{t-s} f(t-n)\quad} (the sum from the first term up to the last is equal to the sum from the last down to the first)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=0}^t f(n) = \sum_{n=0}^{t} f(t-n)\quad} (a particular case of the formula above)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=k_0}^{k_1}\sum_{j=l_0}^{l_1} a_{i,j} = \sum_{j=l_0}^{l_1}\sum_{i=k_0}^{k_1} a_{i,j}\quad} (commutativity and associativity, again)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k\le j \le i\le n} a_{i,j} = \sum_{i=k}^n\sum_{j=k}^i a_{i,j} = \sum_{j=k}^n\sum_{i=j}^n a_{i,j} = \sum_{j=0}^{n-k}\sum_{i=k}^{n-j} a_{i+j,i}\quad} (another application of commutativity and associativity)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=2s}^{2t+1} f(n) = \sum_{n=s}^t f(2n) + \sum_{n=s}^t f(2n+1)\quad} (splitting a sum into its odd and even parts, for even indexes)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=2s+1}^{2t} f(n) = \sum_{n=s+1}^t f(2n) + \sum_{n=s+1}^t f(2n-1)\quad} (splitting a sum into its odd and even parts, for odd indexes)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \biggl(\sum_{i=0}^{n} a_i\biggr) \biggl(\sum_{j=0}^{n} b_j\biggr)=\sum_{i=0}^n \sum_{j=0}^n a_ib_j \quad} (distributivity)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=s}^m\sum_{j=t}^n {a_i}{c_j} = \biggl(\sum_{i=s}^m a_i\biggr) \biggl( \sum_{j=t}^n c_j \biggr)\quad} (distributivity allows factorization)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=s}^t \log_b f(n) = \log_b \prod_{n=s}^t f(n)\quad} (the logarithm of a product is the sum of the logarithms of the factors)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C^{\sum\limits_{n=s}^t f(n) } = \prod_{n=s}^t C^{f(n)}\quad} (the exponential of a sum is the product of the exponential of the summands)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum^{k}_{m = 0}\sum^{m}_{n = 0}f(m,n)=\sum^{k}_{m = 0}\sum^{k}_{n = m}f(n,m),\quad} for any function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle f} from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \mathbb{Z}\times\mathbb{Z}} .

Powers and logarithm of arithmetic progressions

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n c = nc\quad} for every c that does not depend on i

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n i = \sum_{i=1}^n i = \frac{n(n+1)}{2}\qquad} (Sum of the simplest arithmetic progression, consisting of the first n natural numbers.)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n (2i-1) = n^2\qquad} (Sum of first odd natural numbers)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n} 2i = n(n+1)\qquad} (Sum of first even natural numbers)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^{n} \log i = \log n!\qquad} (A sum of logarithms is the logarithm of the product)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n i^2 = \sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6} = \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\qquad} (Sum of the first squares, see square pyramidal number.)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n i^3 = \biggl(\sum_{i=0}^n i \biggr)^2 = \left(\frac{n(n+1)}{2}\right)^2 = \frac{n^4}{4} + \frac{n^3}{2} + \frac{n^2}{4}\qquad} (Nicomachus's theorem)

More generally, one has Faulhaber's formula for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p>1}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=1}^n k^{p} = \frac{n^{p+1}}{p+1} + \frac{1}{2}n^p + \sum_{k=2}^p \binom p k \frac{B_k}{p-k+1}\,n^{p-k+1},}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_k} denotes a Bernoulli number, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \binom p k} is a binomial coefficient.

Summation index in exponents

In the following summations, a is assumed to be different from 1.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n-1} a^i = \frac{1-a^n}{1-a}} (sum of a geometric progression)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n-1} \frac{1}{2^i} = 2-\frac{1}{2^{n-1}}} (special case for a = 1/2)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n-1} i a^i =\frac{a-na^n+(n-1)a^{n+1}}{(1-a)^2}} (a times the derivative with respect to a of the geometric progression)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin {align} \sum_{i= 0}^{n-1} \left(b + i d\right) a^i &= b \sum_{i= 0}^{n-1} a^i + d \sum_{i= 0}^{n-1} i a^i\\ & = b \left(\frac{1-a^n}{1-a}\right) + d \left(\frac{a-na^n+(n-1)a^{n+1}}{(1-a)^2}\right)\\ & = \frac{b(1-a^n) - (n - 1)d a^n}{1 - a}+\frac{da(1 - a^{n - 1})}{(1 - a)^2} \end {align}}

(sum of an arithmetico–geometric sequence)

Binomial coefficients and factorials

Main article: Binomial coefficient § Sums of the binomial coefficients

There exist very many summation identities involving binomial coefficients (a whole chapter of Concrete Mathematics is devoted to just the basic techniques). Some of the most basic ones are the following.

Involving the binomial theorem

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n {n \choose i}a^{n-i} b^i=(a + b)^n,} the binomial theorem

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n {n \choose i} = 2^n,} the special case where a = b = 1

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n {n \choose i}p^i (1-p)^{n-i}=1} , the special case where p = a = 1 − b, which, for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \le p \le 1,} expresses the sum of the binomial distribution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n} i{n \choose i} = n(2^{n-1}),} the value at a = b = 1 of the derivative with respect to a of the binomial theorem

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n \frac{n \choose i}{i+1} = \frac{2^{n+1}-1}{n+1},} the value at a = b = 1 of the antiderivative with respect to a of the binomial theorem

Involving permutation numbers

In the following summations, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {}_{n}P_{k}} is the number of k-permutations of n.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n} {}_{i}P_{k}{n \choose i} = {}_{n}P_{k}(2^{n-k})}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n {}_{i+k}P_{k+1} = \sum_{i=1}^n \prod_{j=0}^k (i+j) = \frac{(n+k+1)!}{(n-1)!(k+2)}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n} i!\cdot{n \choose i} = \sum_{i=0}^{n} {}_{n}P_{i} = \lfloor n! \cdot e \rfloor, \quad n \in \mathbb{Z}^+} , where and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lfloor x\rfloor} denotes the floor function.

Others

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^{m} \binom{n+k}{n} = \binom{n+m+1}{n+1}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=k}^{n} {i \choose k} = {n+1 \choose k+1}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n i\cdot i! = (n+1)! - 1}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n {m+i-1 \choose i} = {m+n \choose n}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n {n \choose i}^2 = {2n \choose n}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^n \frac{1}{i!} = \frac{\lfloor n!\; e \rfloor}{n!}}

Harmonic numbers

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n \frac{1}{i} = H_n\quad} (the nth harmonic number)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n \frac{1}{i^k} = H^k_n\quad} (a generalized harmonic number)

Growth rates

The following are useful approximations (using theta notation):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n i^c \in \Theta(n^{c+1})} for real c greater than −1

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n \frac{1}{i} \in \Theta(\log_e n)} (See Harmonic number)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n c^i \in \Theta(c^n)} for real c greater than 1

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n \log(i)^c \in \Theta(n \cdot \log(n)^{c})} for non-negative real c

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n \log(i)^c \cdot i^d \in \Theta(n^{d+1} \cdot \log(n)^{c})} for non-negative real c, d

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n \log(i)^c \cdot i^d \cdot b^i \in \Theta (n^d \cdot \log(n)^c \cdot b^n)} for non-negative real b > 1, c, d

History

• In 1675, Gottfried Wilhelm Leibniz, in a letter to Henry Oldenburg, suggests the symbol ∫ to mark the sum of differentials (Latin: calculus summatorius), hence the S-shape. The renaming of this symbol to integral arose later in exchanges with Johann Bernoulli.
• In 1755, the summation symbol Σ is attested in Leonhard Euler's Institutiones calculi differentialis. Euler uses the symbol in expressions like:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma \ (2 wx + w^2) = x^2}

• In 1772, usage of Σ and Σⁿ is attested by Lagrange.
• In 1823, the capital letter S is attested as a summation symbol for series. This usage was apparently widespread.
• In 1829, the summation symbol Σ is attested by Fourier and C. G. J. Jacobi. Fourier's use includes lower and upper bounds, for example:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^{\infty}e^{-i^2t} \ldots}

See also

• Capital-pi notation
• Einstein notation
• Iverson bracket
• Iterated binary operation
• Kahan summation algorithm
• Product (mathematics)
• Summation by parts
• Sigma § Character encoding

Bibliography

• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. ISBN 978-0-486-67766-8.

External links

• Media related to Summation at Wikimedia Commons