File:Duffing oscillator.webm
The media handler extension for this file format is missing. Advanced media features may not work unless the file is viewed at Wikimedia Commons.
Size of this preview: 750 × 600 pixels. Other resolutions: 300 × 240 pixels | 600 × 480 pixels | 960 × 768 pixels | 1,280 × 1,024 pixels | 2,000 × 1,600 pixels.
Original file (file size: 30.43 MB, MIME type: video/webm)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionDuffing oscillator.webm |
English: def potential_well(x, a, b):
return - a * x ** 2 + b * x ** 4
def draw_potential_well(potential_well, F, x0, xmin, xmax, ax, safety_factor=0.03):
x = np.linspace(xmin, xmax, 200)
y = potential_well(x)
ymin, ymax = min(y), max(y)
ymin -= (ymax - ymin) * safety_factor
ymax += (ymax - ymin) * safety_factor
ax.plot(x, y, color='gray')
arrow_props = {'width': (ymax-ymin) * 5e-3, 'head_width': (ymax-ymin) * 2e-2,
'head_length': (xmax-xmin) * 2e-2, 'length_includes_head': True,
'facecolor': '#4a5a90', 'edgecolor': 'none'}
ax.arrow(x0, potential_well(x0), F, 0, **arrow_props)
ax.scatter(x0, potential_well(x0), color='#938fba', s=100)
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
return ax
# Code modified from https://github.com/vkulkar/Duffing by Vikram Kulkarni
import numpy as np
import matplotlib.pyplot as plt
# parameters (mass = 1)
a, b = 0.5, 1/16 # potential coefficients
gamma = 0.1 # damping coefficient
F_0 = 2.5 # driving force
omega = 2.0 # driving angular frequency
period = 2*np.pi/omega
cycles, steps_per_cycle = 100000, 65
h = period/steps_per_cycle # time step
# length of the simulation
T = period * cycles
t = np.arange(0,T,h)
def x_2(x,v): return -gamma*v + 2.0*a*x - 4.0*b*x*x*x
def x_3(x2,x,v): return -gamma*x2 + 2.0*a*v -12.0*b*x*x*v
def x_4(x3,x2,x,v): return -gamma*x3 + 2.0*a*x2 -12.0*b*x*x*x2 - 24.0*b*v*v*x
def x_5(x4,x3,x2,x,v): return -gamma*x4 + 2*a*x3 -12.0*b*(x*x*x3 + 2.0*x2*x*v) -24.0*b*(v*v*v+2*x*v*x2)
# Trigonometric terms in derivatives
x2F = F_0*np.cos(omega*t)
x3F = -F_0*omega*np.sin(omega*t)
x4F = -F_0*omega*omega*np.cos(omega*t)
x5F = F_0*omega*omega*omega*np.sin(omega*t)
# Taylor series coefficients
coef1 = 1/2 *h**2
coef2 = 1/6 *h**3
coef3 = 1/24 *h**4
coef4 = 1/120*h**5
# initial conditions
x, v = 0.5, 0.0
position = np.zeros(len(t))
velocity = np.zeros(len(t))
position[0] = x
for i in range(1,len(t)):
d2 = x_2(x,v) + x2F[i]
d3 = x_3(d2,x,v) + x3F[i]
d4 = x_4(d3,d2,x,v) + x4F[i]
d5 = x_5(d4,d3,d2,x,v) + x5F[i]
# Taylor series expansion for x,v. Order h^5
x += v*h + coef1*d2 + coef2*d3 + coef3*d4 + coef4*d5
v += d2*h + coef1*d3 + coef2*d4 + coef3*d5
position[i] = x
velocity[i] = v
def get_lims(tensor, safety_factor = 0.03):
if tensor.shape[1] != 2:
tensor = tensor.T
xmin, xmax = min(tensor[:,0]), max(tensor[:,0])
ymin, ymax = min(tensor[:,1]), max(tensor[:,1])
xmin -= (xmax - xmin) * safety_factor
xmax += (xmax - xmin) * safety_factor
ymin -= (ymax - ymin) * safety_factor
ymax += (ymax - ymin) * safety_factor
return xmin, xmax, ymin, ymax
def plotting(trail, tmin, tmax, t, position, velocity):
xmin, xmax, ymin, ymax = get_lims(np.array([position, velocity]))
fig, axs = plt.subplot_mosaic("AAAAAB;AAAAAC;AAAAAC;AAAAAD", figsize=(20, 16))
# Poincare plot
ax=axs['A']
poincare_plot = np.array([position, velocity]).T[(tmax%steps_per_cycle)::steps_per_cycle,:]
ax.scatter(poincare_plot[:,0],poincare_plot[:,1], color='#938fba', s=2)
ax.set_xticks([])
ax.set_yticks([])
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.set_xlabel('$x$',{'fontsize':16})
ax.set_ylabel('$\dot x$',{'fontsize':16})
# ax.set_title(r'Poincare Plot (Phase space at time = $\frac{2\pi N}{\omega}$, N = 1,2,3...)',{'fontsize':16})
ax.tick_params(axis='both',labelsize=16)
# Vector field plot
x_axis = np.linspace(xmin, xmax, 20)
y_axis = np.linspace(ymin, ymax, 20)
x_values, y_values = np.meshgrid(x_axis, y_axis)
dx = 1.0*y_values
dy = x_2(x_values, y_values) + x2F[tmax]
arrow_lengths = np.sqrt(dx**2 + dy**2)
alpha_values = 1 - (arrow_lengths / np.max(arrow_lengths))**0.4
ax.quiver(x_values, y_values, dx, dy, color='blue', linewidth=0.5, alpha=alpha_values)
# Potential well plot
ax = axs['B']
draw_potential_well(potential_well=(lambda x: potential_well(x, a, b)),
F=x2F[tmax], x0=position[tmax], xmin=xmin, xmax=xmax, ax=ax, safety_factor=0.03)
ax.set_xticks([])
ax.set_yticks([])
ax.set_xlabel('$x$',{'fontsize':16})
ax.set_ylabel('$V(x)$',{'fontsize':16})
# Trajectory plot
ax = axs['C']
ax.plot(position[max(0, tmin):tmax], t[max(0, tmin):tmax], color='#4a5a90', linewidth=1)
ax.scatter(position[tmax], t[tmax], color='#938fba')
ax.set_xticks([])
ax.set_yticks([])
ax.set_xlim(xmin, xmax)
ax.set_ylim((tmin-2)*h, (tmax+2)*h)
# ax.set_title('Trajectory of the oscillator',{'fontsize':16})
ax.set_xlabel('$x$',{'fontsize':16})
ax.set_ylabel('$t$',{'fontsize':16})
ax.tick_params(axis='both',labelsize=16)
# Phase space plot
ax=axs['D']
for j in range(max(0, tmin), tmax):
alpha = (j - (tmax - trail)) / trail
ax.plot(position[j-1:j+1], velocity[j-1:j+1], '.-', markersize=2, color='#4a5a90', alpha=alpha)
ax.set_xticks([])
ax.set_yticks([])
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
# ax.set_title('Phase space',{'fontsize':16})
ax.set_xlim([-4.5,4.5])
ax.set_xlabel('$x$',{'fontsize':16})
ax.set_ylabel('$\dot x$',{'fontsize':16})
ax.tick_params(axis='both',labelsize=16)
fig.suptitle(fr'Duffing, $(\alpha, \beta, \gamma, F_0, \omega) = ({a}, {b}, {gamma}, {F_0}, {omega})$', fontsize=20,y=0.92)
return fig, ax
import imageio.v3 as iio
import os
from natsort import natsorted
import moviepy.editor as mp
def export_to_video(dir_paths, fps=12):
for dir_path in dir_paths:
file_names = natsorted((fn for fn in os.listdir(dir_path) if fn.endswith('.png')))
# Create a list of image files and set the frame rate
images = []
# Iterate over the file names and append the images to the list
for file_name in file_names:
file_path = os.path.join(dir_path, file_name)
images.append(iio.imread(file_path))
filename = dir_path[2:]
iio.imwrite(f"{filename}.gif", images, duration=1000/fps, rewind=True)
clip = mp.ImageSequenceClip(images, fps=fps)
clip.write_videofile(f"{filename}.mp4")
return
from tqdm import trange
import os
for i, tmax in enumerate(trange(0, 10 * steps_per_cycle)):
trail = 3 * steps_per_cycle
tmin = tmax-trail
fig, ax = plotting(trail=trail, tmin=tmin, tmax=tmax, t=t, position=position, velocity=velocity)
dir_path = "./duffing"
if not os.path.exists(dir_path):
os.makedirs(dir_path)
fig.savefig(f"{dir_path}/{i}.png")
plt.close()
export_to_video(["./duffing"], fps=12)
|
| Date | |
| Source | Own work |
| Author | Cosmia Nebula |
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
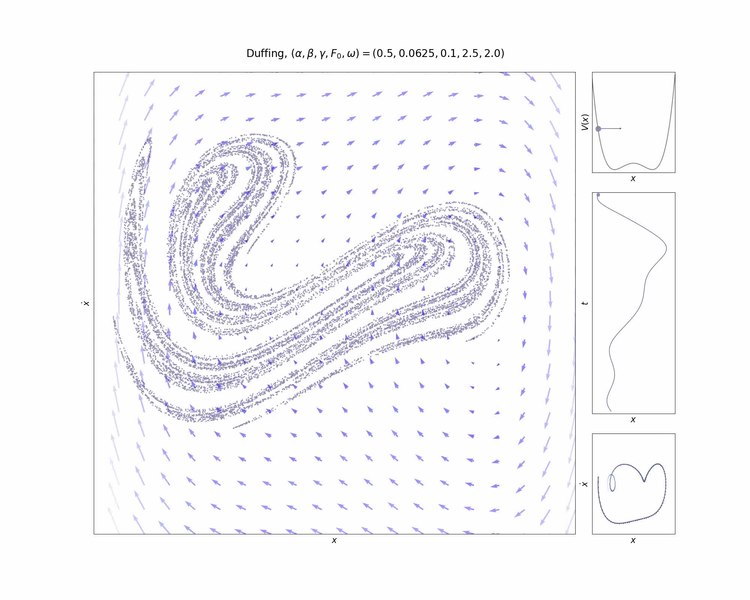
Duffing oscillator plot, containing phase plot, trajectory, strange attractor, Poincare section, and double well potential plot.
Items portrayed in this file
depicts
some value
20 April 2023
video/webm
31,904,392 byte
52 second
1,600 pixel
2,000 pixel
04bc59f51b08bdbf3c2258fb730395abdaccd865
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 07:59, 21 April 2023 |  | (30.43 MB) | wikimediacommons>Cosmia Nebula | Uploaded own work with UploadWizard |
File usage
The following page uses this file:
Retrieved from "https://enwiki.freddythechick.net/wiki/File:Duffing_oscillator.webm"