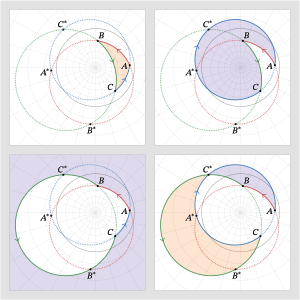
Lexell's theorem

Orange triangles △ABC share a base AB and have the same area. The locus of their variable apex C is a small circle (dashed green) passing through the points antipodal to A and B.

In spherical geometry, Lexell's theorem holds that every spherical triangle with the same surface area on a fixed base has its apex on a small circle, called Lexell's circle or Lexell's locus, passing through each of the two points antipodal to the two base vertices.

A spherical triangle is a shape on a sphere consisting of three vertices (corner points) connected by three sides, each of which is part of a great circle (the analog on the sphere of a straight line in the plane, for example the equator and meridians of a globe). Any of the sides of a spherical triangle can be considered the base, and the opposite vertex is the corresponding apex. Two points on a sphere are antipodal if they are diametrically opposite, as far apart as possible.

The theorem is named for Anders Johan Lexell, who presented a paper about it c. 1777 (published 1784) including both a trigonometric proof and a geometric one. Lexell's colleague Leonhard Euler wrote another pair of proofs in 1778 (published 1797), and a variety of proofs have been written since by Adrien-Marie Legendre (1800), Jakob Steiner (1827), Carl Friedrich Gauss (1841), Paul Serret (1855), and Joseph-Émile Barbier (1864), among others.

The theorem is the analog of propositions 37 and 39 in Book I of Euclid's Elements, which prove that every planar triangle with the same area on a fixed base has its apex on a straight line parallel to the base. An analogous theorem can also be proven for hyperbolic triangles, for which the apex lies on a hypercycle.

Statement

An area formula for spherical triangles analogous to the formula for planar triangles

Given a fixed base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB,} an arc of a great circle on a sphere, and two apex points $C$ and $X$ on the same side of great circle $AB,$ Lexell's theorem holds that the surface area of the spherical triangle $\triangle ABX$ is equal to that of $\triangle ABC$ if and only if $X$ lies on the small-circle arc $B^{*}CA^{*}\!,$ where $A^{*}$ and $B^{*}$ are the points antipodal to $A$ and $B,$ respectively.

As one analog of the planar formula Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{area} = \tfrac12 \, \text{base} \cdot \text{height}} for the area of a triangle, the spherical excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} of spherical triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} can be computed in terms of the base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} (the angular length of arc $AB$) and "height" Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_c} (the angular distance between the parallel small circles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^* B^* C} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A B C^*} ):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \tfrac12 \varepsilon = \tan \tfrac12 c \, \tan\tfrac12 h_c.}

This formula is based on consideration of a sphere of radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , on which arc length is called angle measure and surface area is called spherical excess or solid angle measure. The angle measure of a complete great circle is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi} radians, and the spherical excess of a hemisphere (half-sphere) is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi} steradians, where $\pi$ is the circle constant.

In the limit for triangles much smaller than the radius of the sphere, this reduces to the planar formula.

The small circles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^* B^* C} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A B C^*} each intersect the great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} at an angle of ${\tfrac {1}{2}}\varepsilon .$

Proofs

There are several ways to prove Lexell's theorem, each illuminating a different aspect of the relationships involved.

Isosceles triangles

Lexell's proof by breaking the triangle △A^∗B^∗C into three isosceles triangles

The main idea in Lexell's c. 1777 geometric proof – also adopted by Eugène Catalan (1843), Robert Allardice (1883), Jacques Hadamard (1901), Antoine Gob (1922), and Hiroshi Maehara (1999) – is to split the triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A^* B^* C} into three isosceles triangles with common apex at the circumcenter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} and then chase angles to find the spherical excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} of triangle $\triangle ABC.$ In the figure, points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} are on the far side of the sphere so that we can clearly see their antipodal points and all of Lexell's circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l.}

Let the base angles of the isosceles triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle B^* C P} (shaded red in the figure), $\triangle CA^{*}P$ (blue), and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A^* B^* P} (purple) be respectively Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta.} (In some cases Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} is outside Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A^* B^* C} ; then one of the quantities Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha, \beta, \delta} will be negative.) We can compute the internal angles of $\triangle ABC$ (orange) in terms of these angles: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle A = \pi - \beta - \delta} (the supplement of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle A^*} ) and likewise Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle B = \pi - \alpha - \delta,} and finally Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle C = \alpha + \beta.}

By Girard's theorem the spherical excess of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varepsilon &= \angle A + \angle B + \angle C - \pi \\[3mu] &= (\pi - \beta - \delta) + (\pi - \alpha - \delta) + (\alpha + \beta) - \pi \\[3mu] &= \pi - 2\delta. \end{align}}

If base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} is fixed, for any third vertex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} falling on the same arc of Lexell's circle, the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} and therefore the quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} will not change, so the excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC,} which depends only on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta,} will likewise be constant. And vice versa: if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} remains constant when the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is changed, then so must Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} be, and therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} must be fixed, so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} must remain on Lexell's circle.

Cyclic quadrilateral

Steiner's proof by constructing a cyclic quadrilateral ◻A^∗DB^∗C inside Lexell's circle

Jakob Steiner (1827) wrote a proof in similar style to Lexell's, also using Girard's theorem, but demonstrating the angle invariants in the triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A^* B^* C} by constructing a cyclic quadrilateral inside the Lexell circle, using the property that pairs of opposite angles in a spherical cyclic quadrilateral have the same sum.

Starting with a triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} , let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} be the Lexell circle circumscribing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A^* B^* C,} and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} be another point on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} separated from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} by the great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^* A^*\!.} Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 = \angle C A^* B^*\!,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1 = \angle A^* B^* C,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_2 = \angle B^* A^* D,} $\beta _{2}=\angle DA^{*}B^{*}\!.$

Because the quadrilateral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square A^* D B^* C} is cyclic, the sum of each pair of its opposite angles is equal, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle C + \angle D = {}\!} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 + \alpha_2 + \beta_1 + \beta_2,} or rearranged Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 + \beta_1 - \angle C = {}\!} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle D - \alpha_2 - \beta_2.}

By Girard's theorem the spherical excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varepsilon &= \angle A + \angle B + \angle C - \pi \\[3mu] &= (\pi - \alpha_1) + (\pi - \beta_1) + \angle C - \pi \\[3mu] &= \pi - (\alpha_1 + \beta_1 - \angle C) \\[3mu] &= \pi - (\angle D - \alpha_2 - \beta_2). \end{align}}

The quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle D - \alpha_2 - \beta_2} does not depend on the choice of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C,} so is invariant when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is moved to another point on the same arc of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l.} Therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} is also invariant.

Conversely, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is changed but Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} is invariant, then the opposite angles of the quadrilateral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square A^* D B^* C} will have the same sum, which implies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} lies on the small circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^* D B^*\!.}

Spherical parallelograms

Euler in 1778 proved Lexell's theorem analogously to Euclid's proof of Elements I.35 and I.37, as did Victor-Amédée Lebesgue independently in 1855, using spherical parallelograms – spherical quadrilaterals with congruent opposite sides, which have parallel small circles passing through opposite pairs of adjacent vertices and are in many ways analogous to Euclidean parallelograms. There is one complication compared to Euclid's proof, however: The four sides of a spherical parallelogram are the great-circle arcs through the vertices rather than the parallel small circles. Euclid's proof does not need to account for the small lens-shaped regions sandwiched between the great and small circles, which vanish in the planar case.

Lemma: Two spherical parallelograms with the same base and between the same parallels have equal area.

A lemma analogous to Elements I.35: two spherical parallelograms on the same base and between the same parallels have equal area.

Proof: Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_2D_2} be spherical parallelograms with the great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} (the "midpoint circle") passing through the midpoints of sides Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BC_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AD_1} coinciding with the corresponding midpoint circle in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_2D_2.} Let $F$ be the intersection point between sides Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AD_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BC_1.} Because the midpoint circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is shared, the two top sides Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_2D_2} lie on the same small circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} parallel to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} and antipodal to a small circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l^*} passing through Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B.}

Two arcs of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} are congruent, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_1D_2 \cong C_1C_2,} thus the two curvilinear triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle BC_1C_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle AD_1D_2,} each bounded by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} on the top side, are congruent. Each parallelogram is formed from one of these curvilinear triangles added to the triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABF} and to one of the congruent lens-shaped regions between each top side and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l,} with the curvilinear triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle D_2C_1F} cut away. Therefore the parallelograms have the same area. (As in Elements, the case where the parallelograms do not intersect on the sides is omitted, but can be proven by a similar argument.)

Proof of Lexell's theorem: Given two spherical triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC_2} each with its apex on the same small circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} through points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*\!,} construct new segments Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_2D_2} congruent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} with vertices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_2} on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l.} The two quadrilaterals Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_2D_2} are spherical parallelograms, each formed by pasting together the respective triangle and a congruent copy. By the lemma, the two parallelograms have the same area, so the original triangles must also have the same area.

Proof of the converse: If two spherical triangles have the same area and the apex of the second is assumed to not lie on the Lexell circle of the first, then the line through one side of the second triangle can be intersected with the Lexell circle to form a new triangle which has a different area from the second triangle but the same area as the first triangle, a contradiction. This argument is the same as that found in Elements I.39.

Saccheri quadrilateral

Gauss's proof using a Saccheri quadrilateral

Another proof using the midpoint circle which is more visually apparent in a single picture is due to Carl Friedrich Gauss (1841), who constructs the Saccheri quadrilateral (a quadrilateral with two adjacent right angles and two other equal angles) formed between the side of the triangle and its perpendicular projection onto the midpoint circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m,} which has the same area as the triangle.

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} be the great circle through the midpoints Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_1} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AC} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_2} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BC,} and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A',} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B',} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C'} be the perpendicular projections of the triangle vertices onto Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m.} The resulting pair of right triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle AA'M_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle CC'M_1} (shaded red) have equal angles at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_1} (vertical angles) and equal hypotenuses, so they are congruent; so are the triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle BB'M_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle CC'M_2} (blue). Therefore, the area of triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} is equal to the area of Saccheri quadrilateral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABB'A',} as each consists of one red triangle, one blue triangle, and the green quadrilateral $\square ABM_{2}M_{1}$ pasted together. (If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C'} falls outside the arc Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'B',} then either the red or blue triangles will have negative signed area.) Because the great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m,} and therefore the quadrilateral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABB'A',} is the same for any choice of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} lying on the Lexell circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l,} the area of the corresponding triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} is constant.

Stereographic projection

The stereographic projection maps the sphere to the plane. A designated great circle is mapped onto the primitive circle in the plane, and its poles are mapped to the origin (center of the primitive circle) and the point at infinity, respectively. Every circle on the sphere is mapped to a circle or straight line in the plane, with straight lines representing circles through the second pole. The stereographic projection is conformal, meaning it preserves angles.

Paul Serret's proof by stereographic projection with A projected to the origin

To prove relationships about a general spherical triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC,} without loss of generality vertex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} can be taken as the point which projects to the origin. The sides of the spherical triangle then project to two straight segments and a circular arc. If the tangent lines to the circular side at the other two vertices intersect at point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E,} a planar straight-sided quadrilateral $\square ABEC$ can be formed whose external angle at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is the spherical excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon = \angle A + \angle B + \angle C - \pi} of the spherical triangle. This is sometimes called the Cesàro method of spherical trigonometry, after crystallographer Giuseppe Cesàro who popularized it in two 1905 papers.

Paul Serret (in 1855, a half century before Cesàro), and independently Aleksander Simonič (2019), used Cesàro's method to prove Lexell's theorem. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O} be the center in the plane of the circular arc to which side Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BC} projects. Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square OBEC} is a right kite, so the central angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle BOC} is equal to the external angle at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E,} the triangle's spherical excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon.} Planar angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle BB^*C} is an inscribed angle subtending the same arc, so by the inscribed angle theorem has measure Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac12\varepsilon.} This relationship is preserved for any choice of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} ; therefore, the spherical excess of the triangle is constant whenever Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} remains on the Lexell circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l,} which projects to a line through Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} in the plane. (If the area of the triangle is greater than a half-hemisphere, a similar argument can be made, but the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is no longer internal to the angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle BOC.} )

Perimeter of the polar triangle

Barbier's proof using the perimeter of a polar triangle △A′B′C′, pictured in stereographic projection

Every spherical triangle has a dual, its polar triangle; if triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A'B'C'} (shaded purple) is the polar triangle of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} (shaded orange) then the vertices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'\!, B'\!, C'} are the poles of the respective sides Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BC, CA, AB,} and vice versa, the vertices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A, B, C} are the poles of the sides Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B'C'\!, C'A'\!, A'B'\!.} The polar duality exchanges the sides (central angles) and external angles (dihedral angles) between the two triangles.

Because each side of the dual triangle is the supplement of an internal angle of the original triangle, the spherical excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} is a function of the perimeter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p'} of the dual triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A'B'C'} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varepsilon &= \angle A + \angle B + \angle C - \pi \\[3mu] &= \bigl(\pi - |B'C'|\bigr) + \bigl(\pi - |C'A'|\bigr) + \bigl(\pi - |A'B'|\bigr) - \pi \\[3mu] &= 2\pi - p', \end{align}}

where the notation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |PQ|} means the angular length of the great-circle arc Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PQ.}

In 1854 Joseph-Émile Barbier – and independently László Fejes Tóth (1953) – used the polar triangle in his proof of Lexell's theorem, which is essentially dual to the proof by isosceles triangles above, noting that under polar duality the Lexell circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} circumscribing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A^* B^* C} becomes an excircle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l'} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A'B'C'} (incircle of a colunar triangle) externally tangent to side Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'B'.}

If vertex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is moved along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l,} the side Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'B'} changes but always remains tangent to the same circle $l'.$ Because the arcs from each vertex to either adjacent touch point of an incircle or excircle are congruent, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'T_B \cong A'T_C} (blue segments) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B'T_A \cong B'T_C} (red segments), the perimeter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p'} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} p' &= |A'B'| + |B'C'| + |C'A'| \\[3mu] &= \bigl(|A'T_C| + |B'T_C|\bigr) + |C'B'| + |C'A'| \\[3mu] &= \bigl(|C'A'| + |A'T_B|\bigr) + \bigl(|C'B'| + |B'T_A|\bigr) \\[3mu] &= |C'T_B| + |C'T_A|, \end{align}}

which remains constant, depending only on the circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l'} but not on the changing side Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'B'.} Conversely, if the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} moves off of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l,} the associated excircle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l'} will change in size, moving the points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_B} both toward or both away from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C'^*} and changing the perimeter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p'} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle A'B'C'\!} and thus changing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon.}

The locus of points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} is constant is therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l.}

Trigonometric proofs

Both Lexell (c. 1777) and Euler (1778) included trigonometric proofs in their papers, and several later mathematicians have presented trigonometric proofs, including Adrien-Marie Legendre (1800), Louis Puissant (1842), Ignace-Louis-Alfred Le Cointe (1858), and Joseph-Alfred Serret (1862). Such proofs start from known triangle relations such as the spherical law of cosines or a formula for spherical excess, and then proceed by algebraic manipulation of trigonometric identities.

Opposite arcs of Lexell's circle

The sphere is separated into two hemispheres by the great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB,} and any Lexell circle through Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} is separated into two arcs, one in each hemisphere. If the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} is on the opposite arc from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C,} then the areas of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABX} will generally differ. However, if spherical surface area is interpreted to be signed, with sign determined by boundary orientation, then the areas of triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABX} have opposite signs and differ by the area of a hemisphere.

Lexell suggested a more general framing. Given two distinct non-antipodal points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B,} there are two great-circle arcs joining them: one shorter than a semicircle and the other longer. Given a triple Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B, C} of points, typically Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} is interpreted to mean the area enclosed by the three shorter arcs joining each pair. However, if we allow choice of arc for each pair, then 8 distinct generalized spherical triangles can be made, some with self intersections, of which four might be considered to have the same base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB.}

The eight generalized spherical triangles for vertices A, B, C, shown in stereographic projection, with orange and purple shading representing areas of opposite signs

These eight triangles do not all have the same surface area, but if area is interpreted to be signed, with sign determined by boundary orientation, then those which differ differ by the area of a hemisphere.

In this context, given four distinct, non-antipodal points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} on a sphere, Lexell's theorem holds that the signed surface area of any generalized triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} differs from that of any generalized triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABX} by a whole number of hemispheres if and only if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*\!,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*\!,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} are concyclic.

Special cases

Lunar degeneracy

In the limit as C → B^∗ along Lexell's circle l the triangle △ABC degenerates to the lune (shaded orange or purple) with its side tangent to l (here pictured in stereographic projection).

As the apex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} approaches either of the points antipodal to the base vertices – say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} – along Lexell's circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l,} in the limit the triangle degenerates to a lune tangent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} and tangent to the antipodal small circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l^*} at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B,} and having the same excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} as any of the triangles with apex on the same arc of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l.} As a degenerate triangle, it has a straight angle at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} (i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle A = \pi,} a half turn) and equal angles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = B^* = \tfrac12\varepsilon.}

As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} approaches Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} from the opposite direction (along the other arc of Lexell's circle), in the limit the triangle degenerates to the co-hemispherical lune tangent to the Lexell circle at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} with the opposite orientation and angles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle B = \angle B^\star = \pi - \tfrac12\varepsilon.}

Half-hemisphere area

The area of a spherical triangle is equal to half a hemisphere (excess Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon = \pi} ) if and only if the Lexell circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*B^*C} is orthogonal to the great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB,} that is if arc Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*B^*} is a diameter of circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*B^*C} and arc Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} is a diameter of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ABC^*\!.}

In this case, letting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} be the point diametrically opposed to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} on the Lexell circle Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle A^{*}B^{*}C} then the four triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle BAD,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle CDA,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle DCB} are congruent, and together form a spherical disphenoid Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ABCD} (the central projection of a disphenoid onto a concentric sphere). The eight points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AA^*BB^*CC^*DD^*} are the vertices of a rectangular cuboid.

Related concepts and results

Spherical parallelogram

A spherical parallelogram, showing great circles with solid lines and small circles with dashed lines

A spherical parallelogram is a spherical quadrilateral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABCD} whose opposite sides and opposite angles are congruent (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB \cong CD,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BC \cong DA,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle A = \angle C,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle B = \angle D} ). It is in many ways analogous to a planar parallelogram. The two diagonals Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AC} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BD} bisect each-other and the figure has 2-fold rotational symmetry about the intersection point (so the diagonals each split the parallelogram into two congruent spherical triangles, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC \cong \triangle CDA} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABD \cong \triangle CDB} ); if the midpoints of either pair of opposite sides are connected by a great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} , the four vertices fall on two parallel small circles equidistant from it. More specifically, any vertex (say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} ) of the spherical parallelogram lies at the intersection of the two Lexell circles (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_{cd}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_{da}} ) passing through one of the adjacent vertices and the points antipodal to the other two vertices.

As with spherical triangles, spherical parallelograms with the same base and the apex vertices lying on the same Lexell circle have the same area; see § Spherical parallelograms above. Starting from any spherical triangle, a second congruent triangle can be formed via a (spherical) point reflection across the midpoint of any side. When combined, these two triangles form a spherical parallelogram with twice the area of the original triangle.

Sorlin's theorem (polar dual)

The polar dual to Lexell's theorem, sometimes called Sorlin's theorem after A. N. J. Sorlin who first proved it trigonometrically in 1825, holds that for a spherical trilateral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle abc} with sides on fixed great circles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a, b} (thus fixing the angle between them) and a fixed perimeter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = |a| + |b| + |c|} (where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |a|} means the length of the triangle side Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} ), the envelope of the third side Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} is a small circle internally tangent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a, b} and externally tangent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c,} the excircle to trilateral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle abc.} Joseph-Émile Barbier later wrote a geometrical proof (1864) which he used to prove Lexell's theorem, by duality; see § Perimeter of the polar triangle above.

This result also applies in Euclidean and hyperbolic geometry: Barbier's geometrical argument can be transplanted directly to the Euclidean or hyperbolic plane.

Foliation of the sphere

A foliation of the sphere by Lexell's loci

Lexell's loci for any base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} make a foliation of the sphere (decomposition into one-dimensional leaves). These loci are arcs of small circles with endpoints at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*\!,} on which any intermediate point $C$ is the apex of a triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ABC} of a fixed signed area. That area is twice the signed angle between the Lexell circle and the great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ABA^*B^*} at either of the points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} ; see § Lunar degeneracy above. In the figure, the Lexell circles are in green, except for those whose triangles' area is a multiple of a half hemisphere, which are black, with area labeled; see § Half-hemisphere area above.

These Lexell circles through Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^*} are the spherical analog of the family of Apollonian circles through two points in the plane.

Maximizing spherical triangle area subject to constraints

In 1784 Nicolas Fuss posed and solved the problem of finding the triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} of maximal area on a given base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} with its apex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} on a given great circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g.} Fuss used an argument involving infinitesimal variation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C,} but the solution is also a straightforward corollary of Lexell's theorem: the Lexell circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^*B^*C} through the apex must be tangent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C.}

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} crosses the great circle through Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} at a point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} , then by the spherical analog of the tangent–secant theorem, the angular distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PC} to the desired point of tangency satisfies

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan^2 \tfrac12|PC| = \tan \tfrac12 |PA^*|\,\tan \tfrac12 |PB^*|,}

from which we can explicitly construct the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} has maximum area.

In 1786 Theodor von Schubert posed and solved the problem of finding the spherical triangles of maximum and minimum area of a given base and altitude (the spherical length of a perpendicular dropped from the apex to the great circle containing the base); spherical triangles with constant altitude have their apex on a common small circle (the "altitude circle") parallel to the great circle containing the base. Schubert solved this problem by a calculus-based trigonometric approach to show that the triangle of minimal area has its apex at the nearest intersection of the altitude circle and the perpendicular bisector of the base, and the triangle of maximal area has its apex at the far intersection. However, this theorem is also a straightforward corollary of Lexell's theorem: the Lexell circles through the points antipodal to the base vertices representing the smallest and largest triangle areas are those tangent to the altitude circle. In 2019 Vincent Alberge and Elena Frenkel solved the analogous problem in the hyperbolic plane.

Steiner's theorem on area bisectors

Steiner's theorem: the "equalizers" (area-bisecting arcs through each vertex) of a spherical triangle all intersect in a point S. (This is distinct from the intersection of the medians G.)

In the Euclidean plane, a median of a triangle is the line segment connecting a vertex to the midpoint of the opposite side. The three medians of a triangle all intersect at its centroid. Each median bisects the triangle's area.

On the sphere, a median of a triangle can also be defined as the great-circle arc connecting a vertex to the midpoint of the opposite side. The three medians all intersect at a point, the central projection onto the sphere of the triangle's extrinsic centroid – that is, centroid of the flat triangle containing the three points if the sphere is embedded in 3-dimensional Euclidean space. However, on the sphere the great-circle arc through one vertex and a point on the opposite side which bisects the triangle's area is, in general, distinct from the corresponding median.

Jakob Steiner used Lexell's theorem to prove that these three area-bisecting arcs (which he called "equalizers") all intersect in a point, one possible alternative analog of the planar centroid in spherical geometry. (A different spherical analog of the centroid is the apex of three triangles of equal area whose bases are the sides of the original triangle, the point with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigl(\tfrac13,\tfrac13,\tfrac13\bigr)} as its spherical area coordinates.)

Spherical area coordinates

Mapping from spherical area coordinates to barycentric coordinates in the plane

The barycentric coordinate system for points relative to a given triangle in affine space does not have a perfect analogy in spherical geometry; there is no single spherical coordinate system sharing all of its properties. One partial analogy is spherical area coordinates for a point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} relative to a given spherical triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC,}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \frac{\varepsilon_{PBC}}{\varepsilon_{ABC}}, \frac{\varepsilon_{APC}}{\varepsilon_{ABC}}, \frac{\varepsilon_{ABP}}{\varepsilon_{ABC}} \right),}

where each quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{QRS}} is the signed spherical excess of the corresponding spherical triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle QRS.} These coordinates sum to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1,} and using the same definition in the plane results in barycentric coordinates.

By Lexell's theorem, the locus of points with one coordinate constant is the corresponding Lexell circle. It is thus possible to find the point corresponding to a given triple of spherical area coordinates by intersecting two small circles.

Using their respective spherical area coordinates, any spherical triangle can be mapped to any other, or to any planar triangle, using corresponding barycentric coordinates in the plane. This can be used for polyhedral map projections; for the definition of discrete global grids; or for parametrizing triangulations of the sphere or texture mapping any triangular mesh topologically equivalent to a sphere.

Euclidean plane

Orange triangles △ABC share a base AB and area. The locus of their apex C is a line (dashed green) parallel to the base.

The analog of Lexell's theorem in the Euclidean plane comes from antiquity, and can be found in Book I of Euclid's Elements, propositions 37 and 39, built on proposition 35. In the plane, Lexell's circle degenerates to a straight line (which could be called Lexell's line) parallel to the base.

Elements I.35

Elements I.35 holds that parallelograms with the same base whose top sides are colinear have equal area. Proof: Let the two parallelograms be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_2D_2,} with common base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_1,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_1,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_2,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_2} on a common line parallel to the base, and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} be the intersection between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BC_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AD_2.} Then the two top sides are congruent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_1D_1 \cong C_2D_2} so, adding the intermediate segment to each, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_1C_2 \cong D_1D_2.} Therefore the two triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle BC_1C_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle AD_1D_2} have matching sides so are congruent. Now each of the parallelograms is formed from one of these triangles, added to the triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABF} with the triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle D_2C_1F} cut away, so therefore the two parallelograms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_2D_2} have equal area.

Elements I.37 holds that triangles with the same base and an apex on the same line parallel to the base have equal area. Proof: Let triangles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC_2} each have its apex on the same line Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} parallel to the base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB.} Construct new segments Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_2D_2} congruent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} with vertices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_2} on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l.} The two quadrilaterals Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_1D_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square ABC_2D_2} are parallelograms, each formed by pasting together the respective triangle and a congruent copy. By I.35, the two parallelograms have the same area, so the original triangles must also have the same area.

Elements I.39 is the converse: two triangles of equal area on the same side of the same base have their apexes on a line parallel to the base. Proof: If two triangles have the same base and same area and the apex of the second is assumed to not lie on the line parallel to the base (the "Lexell line") through the first, then the line through one side of the second triangle can be intersected with the Lexell line to form a new triangle which has a different area from the second triangle but the same area as the first triangle, a contradiction.

In the Euclidean plane, the area Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} of triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} can be computed using any side length (the base) and the distance between the line through the base and the parallel line through the apex (the corresponding height). Using point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} as the apex, and multiplying both sides of the traditional identity by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac12} to make the analogy to the spherical case more obvious, this is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac12 \varepsilon = \tfrac12 c\,\tfrac12 h_c.}

The Euclidean theorem can be taken as a corollary of Lexell's theorem on the sphere. It is the limiting case as the curvature of the sphere approaches zero, i.e. for spherical triangles as which are infinitesimal in proportion to the radius of the sphere.

Hyperbolic plane

In the half-plane model, antipodal points are reflections into the opposite half-plane (shaded gray). Hyperbolic triangles △ABC (orange) share a base AB and area. The locus of apex C is a hypercycle (dashed green) passing through points antipodal to A and B.

In the hyperbolic plane, given a triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC,} the locus of a variable point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} such that the triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABX} has the same area as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle ABC} is a hypercycle passing through the points antipodal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B,} which could be called Lexell's hypercycle. Several proofs from the sphere have straightforward analogs in the hyperbolic plane, including a Gauss-style proof via a Saccheri quadrilateral by Barbarin (1902) and Frenkel & Su (2019), an Euler-style proof via hyperbolic parallelograms by Papadopoulos & Su (2017), and a Paul Serret-style proof via stereographic projection by Shvartsman (2007).

In spherical geometry, the antipodal transformation takes each point to its antipodal (diametrically opposite) point. For a sphere embedded in Euclidean space, this is a point reflection through the center of the sphere; for a sphere stereographically projected to the plane, it is an inversion across the primitive circle composed with a point reflection across the origin (or equivalently, an inversion in a circle of imaginary radius of the same magnitude as the radius of the primitive circle).

In planar hyperbolic geometry, there is a similar antipodal transformation, but any two antipodal points lie in opposite branches of a double hyperbolic plane. For a hyperboloid of two sheets embedded in Minkowski space of signature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-, +, +),} known as the hyperboloid model, the antipodal transformation is a point reflection through the center of the hyperboloid which takes each point onto the opposite sheet; in the conformal half-plane model it is a reflection across the boundary line of ideal points taking each point into the opposite half-plane; in the conformal disk model it is an inversion across the boundary circle, taking each point in the disk to a point in its complement. As on the sphere, any generalized circle passing through a pair of antipodal points in hyperbolic geometry is a geodesic.

Analogous to the planar and spherical triangle area formulas, the hyperbolic area Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} of the triangle can be computed in terms of the base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} (the hyperbolic length of arc Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB} ) and "height" Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_c} (the hyperbolic distance between the parallel hypercycles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^* B^* C} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A B C^*} ):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \tfrac12 \varepsilon = \tanh\tfrac12 c \, \tanh\tfrac12 h_c.}

As in the spherical case, in the small-triangle limit this reduces to the planar formula.

References

• Atzema, Eisso J. (2017), "'A Most Elegant Property': On the Early History of Lexell's Theorem", in Zack, Maria; Schlimm, Dirk (eds.), Research in History and Philosophy of Mathematics, CSHPM 2016, Calgary, Alberta, Birkhäuser, pp. 117–132, doi:10.1007/978-3-319-64551-3_8
• Casey, John (1889), A treatise on spherical trigonometry, and its application to geodesy and astronomy, with numerous examples, Dublin: Hodges, Figgis, & Co.
• Euler, Leonhard (1797) [written 1778], "Variae speculationes super area triangulorum sphaericorum", Nova Acta Academiae Scientiarum Imperialis Petropolitanae (in Latina), 10: 47–62, figures tab. 1, E698, in Opera omnia, ser. 1, vol. 29, pp. 253–266, translated as "Different Speculations on the Area of Spherical Triangles" (PDF), 17centurymaths.com, translated by Stén, Johan Carl-Erik, 2008
• Lexell, Anders Johan (1784) [written c. 1777], "Solutio problematis geometrici ex doctrina sphaericorum", Acta Academiae Scientarum Imperialis Petropolitinae (in Latina), 5: 1781 (1): 112–126, figures tab. 4, translated as "Solution of a geometrical problem from the theory of the sphere" (PDF), 17centurymaths.com, translated by Stén, Johan Carl-Erik, 2009
• Maehara, Hiroshi; Martini, Horst (2023), "Seven Proofs of Lexell's Theorem: An Excursion into Spherical Geometry", Mathematical Intelligencer, doi:10.1007/s00283-023-10281-7
• Papadopoulos, Athanase (2014), "On the works of Euler and his followers on spherical geometry", Gaṇita Bhārati, 36: 53–108, arXiv:1409.4736
• Stén, Johan Carl-Erik (2014), A Comet of the Enlightenment: Anders Johan Lexell's Life and Discoveries, Birkhäuser, doi:10.1007/978-3-319-00618-5
• Todhunter, Isaac; Leathem, John Gaston (1901), Spherical Trigonometry (Revised ed.), MacMillan
• Zhukova, Alena M. (2019), "On the Contribution of Anders Johan Lexell in Spherical Geometry", Gaṇita Bhārati, 41 (1–2): 127–149, doi:10.32381/GB.2019.41.1-2.5, ProQuest 2561520777