Many-sorted logic

Many-sorted logic can reflect formally our intention not to handle the universe as a homogeneous collection of objects, but to partition it in a way that is similar to types in typeful programming. Both functional and assertive "parts of speech" in the language of the logic reflect this typeful partitioning of the universe, even on the syntax level: substitution and argument passing can be done only accordingly, respecting the "sorts".

There are various ways to formalize the intention mentioned above; a many-sorted logic is any package of information which fulfils it. In most cases, the following are given:

a set of sorts, S
an appropriate generalization of the notion of signature to be able to handle the additional information that comes with the sorts.

The domain of discourse of any structure of that signature is then fragmented into disjoint subsets, one for every sort.

Example

When reasoning about biological organisms, it is useful to distinguish two sorts: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm {plant} } and $\mathrm {animal}$ . While a function $\mathrm {mother} \colon \mathrm {animal} \to \mathrm {animal}$ makes sense, a similar function $\mathrm {mother} \colon \mathrm {plant} \to \mathrm {plant}$ usually does not. Many-sorted logic allows one to have terms like $\mathrm {mother} (\mathrm {lassie} )$ , but to discard terms like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm {mother} (\mathrm {my\_favorite\_oak} )} as syntactically ill-formed.

Algebraization

The algebraization of many-sorted logic is explained in an article by Caleiro and Gonçalves,^[1] which generalizes abstract algebraic logic to the many-sorted case, but can also be used as introductory material.

Order-sorted logic

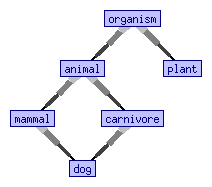
While many-sorted logic requires two distinct sorts to have disjoint universe sets, order-sorted logic allows one sort Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{1}} to be declared a subsort of another sort Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{2}} , usually by writing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{1}\subseteq s_{2}} or similar syntax. In the above biology example, it is desirable to declare

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{dog}}\subseteq {\text{carnivore}}} ,

{\text{dog}}\subseteq {\text{mammal}}

,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{carnivore}}\subseteq {\text{animal}}} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{mammal}}\subseteq {\text{animal}}} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{animal}}\subseteq {\text{organism}}} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{plant}}\subseteq {\text{organism}}} ,

and so on; cf. picture.

Wherever a term of some sort Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} is required, a term of any subsort of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} may be supplied instead (Liskov substitution principle). For example, assuming a function declaration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{mother}}:{\text{animal}}\longrightarrow {\text{animal}}} , and a constant declaration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{lassie}}:{\text{dog}}} , the term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{mother}}({\text{lassie}})} is perfectly valid and has the sort Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{animal}}} . In order to supply the information that the mother of a dog is a dog in turn, another declaration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{mother}}:{\text{dog}}\longrightarrow {\text{dog}}} may be issued; this is called function overloading, similar to overloading in programming languages.

Order-sorted logic can be translated into unsorted logic, using a unary predicate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{i}(x)} for each sort $s_{i}$ , and an axiom Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \forall x(p_{i}(x)\rightarrow p_{j}(x))} for each subsort declaration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{i}\subseteq s_{j}} . The reverse approach was successful in automated theorem proving: in 1985, Christoph Walther could solve a then benchmark problem by translating it into order-sorted logic, thereby boiling it down an order of magnitude, as many unary predicates turned into sorts.^[2]

In order to incorporate order-sorted logic into a clause-based automated theorem prover, a corresponding order-sorted unification algorithm is necessary, which requires for any two declared sorts Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{1},s_{2}} their intersection Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{1}\cap s_{2}} to be declared, too: if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{1}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{2}} are variables of sort Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{1}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{2}} , respectively, the equation $x_{1}{\stackrel {?}{=}}\,x_{2}$ has the solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{x_{1}=x,\;x_{2}=x\}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x:s_{1}\cap s_{2}} .

Smolka generalized order-sorted logic to allow for parametric polymorphism.^[3]^[4] In his framework, subsort declarations are propagated to complex type expressions. As a programming example, a parametric sort Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{list}}(X)} may be declared (with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} being a type parameter as in a C++ template), and from a subsort declaration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{int}}\subseteq {\text{float}}} the relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{list}}({\text{int}})\subseteq {\text{list}}({\text{float}})} is automatically inferred, meaning that each list of integers is also a list of floats.

Schmidt-Schauß generalized order-sorted logic to allow for term declarations.^[5] As an example, assuming subsort declarations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{even}}\subseteq {\text{int}}} and ${\text{odd}}\subseteq {\text{int}}$ , a term declaration like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \forall i:{\text{int}}.\;(i+i):{\text{even}}} allows to declare a property of integer addition that could not be expressed by ordinary overloading.

References

^ Carlos Caleiro, Ricardo Gonçalves (2006). "On the algebraization of many-sorted logics". Proc. 18th int. conf. on Recent trends in algebraic development techniques (WADT) (PDF). Springer. pp. 21–36. ISBN 978-3-540-71997-7.
^ Walther, Christoph (1985). "A Mechanical Solution of Schubert's Steamroller by Many-Sorted Resolution" (PDF). Artif. Intell. 26 (2): 217–224. doi:10.1016/0004-3702(85)90029-3.
^ Smolka, Gert (Nov 1988). "Logic Programming with Polymorphically Order-Sorted Types". Int. Workshop Algebraic and Logic Programming. LNCS. Vol. 343. Springer. pp. 53–70.
^ Smolka, Gert (May 1989), Logic Programming over Polymorphically Order-Sorted Types (Ph.D. thesis), University of Kaiserslautern-Landau, Germany
^ Schmidt-Schauß, Manfred (Apr 1988). Computational Aspects of an Order-Sorted Logic with Term Declarations. LNAI. Vol. 395. Springer.

Early papers on many-sorted logic include:

Wang, Hao (1952). "Logic of many-sorted theories". Journal of Symbolic Logic. 17 (2): 105–116. doi:10.2307/2266241. JSTOR 2266241., collected in the author's Computation, Logic, Philosophy. A Collection of Essays, Beijing: Science Press; Dordrecht: Kluwer Academic, 1990.
Gilmore, P.C. (1958). "An addition to "Logic of many-sorted theories"" (PDF). Compositio Mathematica. 13: 277–281.
A. Oberschelp (1962). "Untersuchungen zur mehrsortigen Quantorenlogik". Mathematische Annalen. 145 (4): 297–333. doi:10.1007/bf01396685. S2CID 123363080. Archived from the original on 2015-02-20. Retrieved 2013-09-11.
F. Jeffry Pelletier (1972). "Sortal Quantification and Restricted Quantification" (PDF). Philosophical Studies. 23 (6): 400–404. doi:10.1007/bf00355532. S2CID 170303654.

External links

"Many-sorted Logic", the first chapter in Lecture Notes on Decision Procedures by Calogero G. Zarba

[1] Carlos Caleiro, Ricardo Gonçalves (2006). "On the algebraization of many-sorted logics". Proc. 18th int. conf. on Recent trends in algebraic development techniques (WADT) (PDF). Springer. pp. 21–36. ISBN 978-3-540-71997-7.

[2] Walther, Christoph (1985). "A Mechanical Solution of Schubert's Steamroller by Many-Sorted Resolution" (PDF). Artif. Intell. 26 (2): 217–224. doi:10.1016/0004-3702(85)90029-3.

[3] Smolka, Gert (Nov 1988). "Logic Programming with Polymorphically Order-Sorted Types". Int. Workshop Algebraic and Logic Programming. LNCS. Vol. 343. Springer. pp. 53–70.

[4] Smolka, Gert (May 1989), Logic Programming over Polymorphically Order-Sorted Types (Ph.D. thesis), University of Kaiserslautern-Landau, Germany

[5] Schmidt-Schauß, Manfred (Apr 1988). Computational Aspects of an Order-Sorted Logic with Term Declarations. LNAI. Vol. 395. Springer.

[1]

[2]

[3]

[4]

[5]

Example

Algebraization

Order-sorted logic

See also

References

External links