Toroidal coordinates

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci $F_{1}$ and $F_{2}$ in bipolar coordinates become a ring of radius $a$ in the $xy$ plane of the toroidal coordinate system; the $z$ -axis is the axis of rotation. The focal ring is also known as the reference circle.

Definition

The most common definition of toroidal coordinates $(\tau ,\sigma ,\phi )$ is

Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x=a\ {\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}\cos \phi }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = a \ \frac{\sinh \tau}{\cosh \tau - \cos \sigma} \sin \phi }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = a \ \frac{\sin \sigma}{\cosh \tau - \cos \sigma} }

together with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{sign}(\sigma)=\mathrm{sign}(z} ). The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} coordinate of a point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} equals the angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{1} P F_{2}} and the $\tau$ coordinate equals the natural logarithm of the ratio of the distances Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{1}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{2}} to opposite sides of the focal ring

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau = \ln \frac{d_{1}}{d_{2}}. }

The coordinate ranges are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\pi<\sigma\le\pi} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau\ge 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\le\phi < 2\pi.}

Coordinate surfaces

Surfaces of constant $\sigma$ correspond to spheres of different radii

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( x^{2} + y^{2} \right) + \left( z - a \cot \sigma \right)^{2} = \frac{a^{2}}{\sin^{2} \sigma} }

that all pass through the focal ring but are not concentric. The surfaces of constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} are non-intersecting tori of different radii

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^{2} + \left( \sqrt{x^{2} + y^{2}} - a \coth \tau \right)^{2} = \frac{a^{2}}{\sinh^{2} \tau} }

that surround the focal ring. The centers of the constant-Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} spheres lie along the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} -axis, whereas the constant- $\tau$ tori are centered in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy} plane.

Inverse transformation

The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\sigma, \tau, \phi)} coordinates may be calculated from the Cartesian coordinates (x, y, z) as follows. The azimuthal angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} is given by the formula

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan \phi = \frac{y}{x} }

The cylindrical radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} of the point P is given by

\rho ^{2}=x^{2}+y^{2}=\left(a{\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}\right)^{2}

and its distances to the foci in the plane defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{1}^{2} = (\rho + a)^{2} + z^{2} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{2}^{2} = (\rho - a)^{2} + z^{2} }

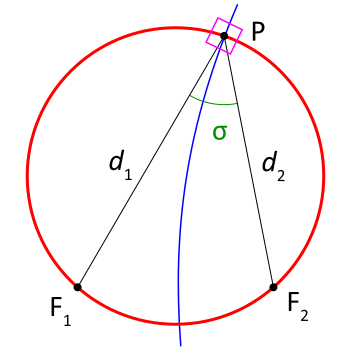
The coordinate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} equals the natural logarithm of the focal distances

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau = \ln \frac{d_{1}}{d_{2}} }

whereas Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\sigma|} equals the angle between the rays to the foci, which may be determined from the law of cosines

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \sigma = \frac{ d_{1}^{2} + d_{2}^{2} - 4 a^{2} }{2 d_{1} d_{2}}. }

Or explicitly, including the sign,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \mathrm{sign}(z)\arccos \frac{r^2-a^2}{\sqrt{(r^2-a^2)^2+4a^2z^2}} }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\sqrt{\rho^2+z^2} } .

The transformations between cylindrical and toroidal coordinates can be expressed in complex notation as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z+i\rho \ = ia\coth\frac{\tau+i\sigma}{2} , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau+i\sigma \ = \ln\frac{ z+i(\rho+a) }{z+i(\rho-a)}. }

Scale factors

The scale factors for the toroidal coordinates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} and $\tau$ are equal

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_\sigma = h_\tau = \frac{a}{\cosh \tau - \cos\sigma} }

whereas the azimuthal scale factor equals

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_\phi = \frac{a \sinh \tau}{\cosh \tau - \cos\sigma} }

Thus, the infinitesimal volume element equals

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dV = \frac{a^3 \sinh \tau}{\left( \cosh \tau - \cos\sigma \right)^3} \, d\sigma \, d\tau \, d\phi }

Differential Operators

The Laplacian is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \nabla^2 \Phi = \frac{\left( \cosh \tau - \cos\sigma \right)^{3}}{a^{2}\sinh \tau} & \left[ \sinh \tau \frac{\partial}{\partial \sigma} \left( \frac{1}{\cosh \tau - \cos\sigma} \frac{\partial \Phi}{\partial \sigma} \right) \right. \\[8pt] & {} \quad + \left. \frac{\partial}{\partial \tau} \left( \frac{\sinh \tau}{\cosh \tau - \cos\sigma} \frac{\partial \Phi}{\partial \tau} \right) + \frac{1}{\sinh \tau \left( \cosh \tau - \cos\sigma \right)} \frac{\partial^2 \Phi}{\partial \phi^2} \right] \end{align}}

For a vector field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{n}(\tau,\sigma,\phi) = n_{\tau}(\tau,\sigma,\phi)\hat{e}_{\tau} + n_{\sigma}(\tau,\sigma,\phi) \hat{e}_{\sigma} + n_{\phi} (\tau,\sigma,\phi) \hat{e}_{\phi},} the Vector Laplacian is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Delta \vec{n}(\tau,\sigma,\phi) &= \nabla (\nabla \cdot \vec{n}) - \nabla \times (\nabla \times \vec{n}) \\ &= \frac{1}{a^2}\vec{e}_{\tau} \left \{ n_{\tau} \left( -\frac{\sinh^4 \tau + (\cosh \tau - \cos \sigma)^2}{\sinh^2 \tau} \right) + n_{\sigma} (- \sinh \tau \sin \sigma ) + \frac{\partial n_{\tau}}{\partial \tau} \left( \frac{(\cosh \tau - \cos \sigma)(1 - \cosh \tau \cos \sigma)}{\sinh \tau} \right) + \cdots \right. \\ &\qquad + \frac{\partial n_{\tau}}{\partial \sigma} ( -(\cosh \tau - \cos \sigma) \sin \sigma ) + \frac{\partial n_{\sigma}}{\partial \sigma} ( 2(\cosh \tau - \cos \sigma) \sinh \tau ) + \frac{\partial n_{\sigma}}{\partial \tau} ( -2(\cosh \tau - \cos \sigma) \sin \sigma ) + \cdots \\ &\qquad + \frac{\partial n_{\phi}}{\partial \phi} \left( \frac{-2(\cosh \tau - \cos \sigma)(1 - \cosh \tau \cos \sigma)}{\sinh^2 \tau} \right) + \frac{\partial^2 n_{\tau}}{{\partial \tau}^2} (\cosh \tau - \cos \sigma)^2 + \frac{\partial^2 n_{\tau}}{{\partial \sigma}^2} (- (\cosh \tau - \cos \sigma)^2 ) + \cdots \\ & \qquad \left. + \frac{\partial^2 n_{\tau}}{{\partial \phi}^2} \frac{(\cosh \tau - \cos \sigma)^2}{\sinh^2 \tau} \right \}\\ &+ \frac{1}{a^2}\vec{e}_{\sigma} \left \{ n_{\tau} \left( -\frac{(\cosh^2 \tau + 1 -2\cosh \tau \cos \sigma)\sin \sigma}{\sinh \tau} \right) + n_{\sigma} \left( - \sinh^2 \tau - 2\sin^2 \sigma \right) + \ldots \right.\\ &\qquad \left. + \frac{\partial n_{\tau}}{\partial \tau} (2 \sin \sigma (\cosh \tau - \cos \sigma) ) + \frac{\partial n_{\tau}}{\partial \sigma} \left( -2 \sinh \tau (\cosh \tau - \cos \sigma) \right) + \cdots \right.\\ &\qquad \left. + \frac{\partial n_{\sigma}}{\partial \tau} \left( \frac{(\cosh \tau - \cos \sigma) (1 - \cosh \tau \cos \sigma) }{\sinh \tau} \right) + \frac{\partial n_{\sigma}}{\partial \sigma} ( -(\cosh \tau - \cos \sigma)\sin \sigma) + \cdots \right.\\ &\qquad \left. + \frac{\partial n_{\phi}}{\partial \phi} \left( 2\frac{(\cosh \tau - \cos \sigma)\sin \sigma}{\sinh \tau} \right) + \frac{\partial^2 n_{\sigma}}{{\partial \tau}^2} (\cosh \tau - \cos \sigma)^2 + \frac{\partial^2 n_{\sigma}}{{\partial \sigma}^2} (\cosh \tau - \cos \sigma)^2 + \cdots \right.\\ &\qquad \left. + \frac{\partial^2 n_{\sigma}}{{\partial \phi}^2} \left( \frac{(\cosh \tau - \cos \sigma)^2}{\sinh^2 \tau} \right) \right \}\\ &+ \frac{1}{a^2}\vec{e}_{\phi} \left \{ n_{\phi} \left( -\frac{(\cosh \tau - \cos \sigma)^2}{\sinh^2 \tau} \right) + \frac{\partial n_{\tau}}{\partial \phi} \left( \frac{2(\cosh \tau - \cos \sigma)(1 - \cosh \tau \cos \sigma)}{\sinh^2 \tau} \right) + \cdots \right.\\ &\qquad \left. + \frac{\partial n_{\sigma}}{\partial \phi} \left( -\frac{2(\cosh \tau - \cos \sigma) \sin \sigma}{\sinh \tau} \right) + \frac{\partial n_{\phi}}{\partial \tau} \left( \frac{(\cosh \tau - \cos \sigma)(1 - \cosh \tau \cos \sigma)}{\sinh \tau} \right) + \cdots \right.\\ &\qquad \left. + \frac{\partial n_{\phi}}{\partial \sigma} (-(\cosh \tau - \cos \sigma) \sin \sigma ) + \frac{\partial^2 n_{\phi}}{{\partial \tau}^2} (\cosh \tau - \cos \sigma)^2 + \cdots \right. \\ &\qquad \left. + \frac{\partial^2 n_{\phi}}{{\partial \sigma}^2} (\cosh \tau - \cos \sigma)^2 + \frac{\partial^2 n_{\phi}}{{\partial \phi}^2} \left( \frac{(\cosh \tau - \cos \sigma)^2}{\sinh^2 \tau} \right) \right \} \end{align}}

Other differential operators such as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \cdot \mathbf{F}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \times \mathbf{F}} can be expressed in the coordinates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\sigma, \tau, \phi)} by substituting the scale factors into the general formulae found in orthogonal coordinates.

Toroidal harmonics

Standard separation

The 3-variable Laplace equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^2\Phi=0}

admits solution via separation of variables in toroidal coordinates. Making the substitution

\Phi =U{\sqrt {\cosh \tau -\cos \sigma }}

A separable equation is then obtained. A particular solution obtained by separation of variables is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi= \sqrt{\cosh\tau-\cos\sigma}\,\,S_\nu(\sigma)T_{\mu\nu}(\tau)V_\mu(\phi)}

where each function is a linear combination of:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_\nu(\sigma)=e^{i\nu\sigma}\,\,\,\,\mathrm{and}\,\,\,\,e^{-i\nu\sigma} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{\mu\nu}(\tau)=P_{\nu-1/2}^\mu(\cosh\tau)\,\,\,\,\mathrm{and}\,\,\,\,Q_{\nu-1/2}^\mu(\cosh\tau) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_\mu(\phi)=e^{i\mu\phi}\,\,\,\,\mathrm{and}\,\,\,\,e^{-i\mu\phi} }

Where P and Q are associated Legendre functions of the first and second kind. These Legendre functions are often referred to as toroidal harmonics.

Toroidal harmonics have many interesting properties. If you make a variable substitution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\cosh\tau>1} then, for instance, with vanishing order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=0} (the convention is to not write the order when it vanishes) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu=0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q_{-\frac12}(z)=\sqrt{\frac{2}{1+z}}K\left(\sqrt{\frac{2}{1+z}}\right)}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{-\frac12}(z)=\frac{2}{\pi}\sqrt{\frac{2}{1+z}}K \left( \sqrt{\frac{z-1}{z+1}} \right)}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\!K} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\!E} are the complete elliptic integrals of the first and second kind respectively. The rest of the toroidal harmonics can be obtained, for instance, in terms of the complete elliptic integrals, by using recurrence relations for associated Legendre functions.

The classic applications of toroidal coordinates are in solving partial differential equations, e.g., Laplace's equation for which toroidal coordinates allow a separation of variables or the Helmholtz equation, for which toroidal coordinates do not allow a separation of variables. Typical examples would be the electric potential and electric field of a conducting torus, or in the degenerate case, an electric current-ring (Hulme 1982).

An alternative separation

Alternatively, a different substitution may be made (Andrews 2006)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi=\frac{U}{\sqrt{\rho}} }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\sqrt{x^2+y^2}=\frac{a\sinh\tau}{\cosh\tau-\cos\sigma}. }

Again, a separable equation is obtained. A particular solution obtained by separation of variables is then:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi= \frac{a}{\sqrt{\rho}}\,\,S_\nu(\sigma)T_{\mu\nu}(\tau)V_\mu(\phi)}

where each function is a linear combination of:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_\nu(\sigma)=e^{i\nu\sigma}\,\,\,\,\mathrm{and}\,\,\,\,e^{-i\nu\sigma} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{\mu\nu}(\tau)=P_{\mu-1/2}^\nu(\coth\tau)\,\,\,\,\mathrm{and}\,\,\,\,Q_{\mu-1/2}^\nu(\coth\tau) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_\mu(\phi)=e^{i\mu\phi}\,\,\,\,\mathrm{and}\,\,\,\,e^{-i\mu\phi}. }

Note that although the toroidal harmonics are used again for the T function, the argument is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \coth\tau} rather than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cosh\tau} and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} indices are exchanged. This method is useful for situations in which the boundary conditions are independent of the spherical angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} , such as the charged ring, an infinite half plane, or two parallel planes. For identities relating the toroidal harmonics with argument hyperbolic cosine with those of argument hyperbolic cotangent, see the Whipple formulae.

References

Byerly, W E. (1893) An elementary treatise on Fourier's series and spherical, cylindrical, and ellipsoidal harmonics, with applications to problems in mathematical physics Ginn & co. pp. 264–266
Arfken G (1970). Mathematical Methods for Physicists (2nd ed.). Orlando, FL: Academic Press. pp. 112–115.
Andrews, Mark (2006). "Alternative separation of Laplace's equation in toroidal coordinates and its application to electrostatics". Journal of Electrostatics. 64 (10): 664–672. CiteSeerX 10.1.1.205.5658. doi:10.1016/j.elstat.2005.11.005.
Hulme, A. (1982). "A note on the magnetic scalar potential of an electric current-ring". Mathematical Proceedings of the Cambridge Philosophical Society. 92 (1): 183–191. doi:10.1017/S0305004100059831.

Bibliography

Morse P M, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw–Hill. p. 666.
Korn G A, Korn T M (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 182. LCCN 59014456.
Margenau H, Murphy G M (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 190–192. LCCN 55010911.
Moon P H, Spencer D E (1988). "Toroidal Coordinates (η, θ, ψ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (2nd ed., 3rd revised printing ed.). New York: Springer Verlag. pp. 112–115 (Section IV, E4Ry). ISBN 978-0-387-02732-6.

External links

MathWorld description of toroidal coordinates

v t e Orthogonal coordinate systems
Two dimensional	Cartesian Polar (Log-polar) Parabolic Bipolar Elliptic
Three dimensional	Cartesian Cylindrical Spherical Parabolic Paraboloidal Oblate spheroidal Prolate spheroidal Ellipsoidal Elliptic cylindrical Toroidal Bispherical Bipolar cylindrical Conical 6-sphere